Distributions discrètes
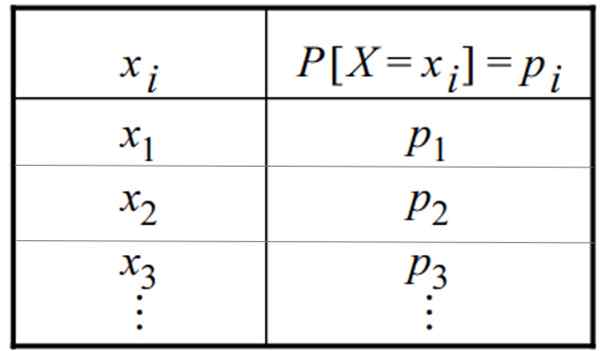
- 3337
- 453
- Raphaël Meyer
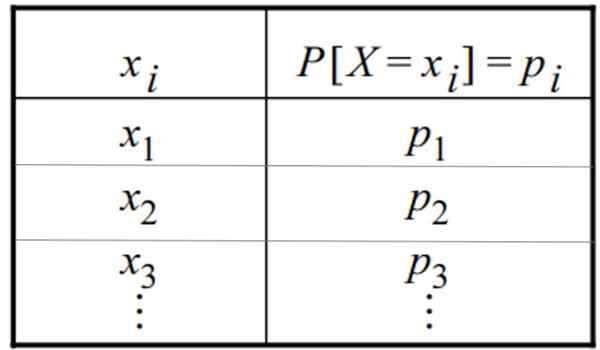 Tableau d'une distribution de probabilité discrète. Source: F. Zapata
Tableau d'une distribution de probabilité discrète. Source: F. Zapata Qu'est-ce qu'une distribution discrète?
Ongle distribution discrète de probabilités est une fonction f (xToi) qui attribue à chaque valeur d'une variable discrète: x1, X2, X3,... XToi, une certaine occurrence de l'occurrence p (x = xToi). Cette fonction est également connue sous le nom de "fonction de masse de probabilité".
La distribution de probabilité discrète peut être donnée sous la forme d'un tableau ou de graphiques. Un tableau a cette forme générale, dans laquelle la variable apparaît dans une colonne et sa probabilité respective dans l'autre:
Les fonctions de masse de probabilité partagent les caractéristiques générales suivantes:
- La probabilité pToi de tout événement xToi Il se situe entre 0 et 1, étant même certaines de ces valeurs limites: 0 ≤ x ≤ 1.
- P (x = xToi) = pToi Prenez simplement des valeurs positives donc: p (x = xToi) ≥ 0.
- Il est vrai que ∑ p (xToi) = 1 pour toutes les valeurs possibles de x.
Une distribution de probabilités décrit le comportement d'une population, décrite par ses paramètres: la moyenne μ, la variance σ2 et l'écart type s = σ σ2.
Ensuite, les distributions discrètes les plus notables sont brièvement décrites:
Distribution uniforme
C'est la distribution discrète la plus simple de tous. En elle la variable peut prendre des valeurs discrètes "n": x1, X2, X3,... XToi, Le tout avec la même probabblaty. Dans ce cas, la distribution est donnée par:
Distribution binomiale
Il s'applique aux expériences avec seulement deux résultats possibles et mutuellement exclusifs, qui sont généralement appelés «succès» et «échec», indiqué respectivement E et F. Le fait qu'un événement s'appelle «succès» ne signifie pas nécessairement que c'est une bonne chose, c'est plutôt une désignation arbitraire.
La probabilité de succès p (e) dans les répétitions «n», est notée p, et celle de l'échec p (f) comme q = 1 - p.
Si "x" représente un certain nombre de succès dans les essais indépendants "n", il est vrai que: 0 ≤ x ≤ n. Et la probabilité d'occurrence P (x) de l'événement est calculée à travers la formule suivante:
Il peut vous servir: des centimètres carrés à des mètres carrés (cm² à m²)Où x = 0, 1, 2, 3 ..., n et le symbole (!) signifie "factoriel":
X! = x ∙ (x - 1) ∙ (x - 2) ∙ (x - 3)… 1
0! = 1
Distribution de Poisson
Dans cette distribution, la variable aléatoire X indique combien de fois un événement se produit dans un intervalle, qui peut être de temps, de distance ou autre. Les occurrences de l'événement sont aléatoires, indépendantes et sont réparties uniformément tout au long de l'intervalle en question.
Une fois ces conditions, la probabilité, qui dépend de la moyenne des occurrences μ et du nombre d'euler ou de nombre «E», sont calculées par:
Les chances des événements avec cette distribution sont faibles, il est donc appelé la "loi des rares affaires".
Approche de la distribution binomiale
La distribution de Poisson est une approche de la distribution binomiale lorsque n est grand (n≥ 100) et P est petit (np ≤ 10). Dans ce cas, la moyenne μ est calculée comme suit:
μ = N ∙ P
Distribution hypergéométrique
Il est utilisé lorsque les probabilités ne sont pas indépendantes, c'est-à-dire après avoir effectué l'expérience, les conditions ne sont plus les mêmes. C'est ce qui se passe lors de l'extraction d'échantillons sans remplacement d'une population, de sorte que la distribution binomiale ne peut plus être utilisée.
Si la population se compose de deux types d'objets différents de et b, et aux objets aléatoires et sans remplacement, la probabilité d'obtenir X objets de type A est:
Où a et b sont les quantités respectives d'objets de chaque type, présents dans la population.
Cependant, si la population est très grande, même s'il n'y a pas de remplacement, il est difficile pour le même élément d'être sélectionné plus d'une fois, donc les deux distributions: binomial et hypergéométrique, produisent des résultats similaires.
Peut vous servir: différence de cubes: formules, équations, exemples, exercicesExemples
Coins lance
Les co -tières sont des exemples très illustratifs:
-Le lancement d'une monnaie honnête et obtenez un visage. On sait que 1 face a une ½ probabilité de départ et la croix (0 face), la même. La distribution est indiquée dans ce tableau:
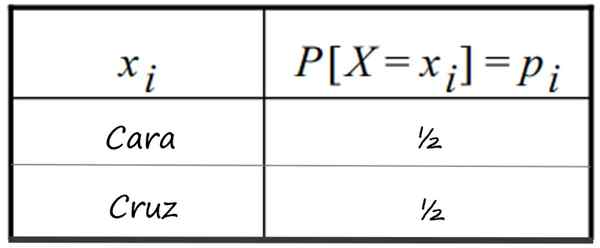 Tableau de distribution de probabilités discrets qui suit le lancement de 1 devise honnête. Source: F. Zapata
Tableau de distribution de probabilités discrets qui suit le lancement de 1 devise honnête. Source: F. Zapata -La photo simultanée de deux pièces honnêtes et nombres de visages possibles qui peuvent être obtenus.
 Tableau de distribution de probabilité discrets qui suit le lancement de deux devises honnêtes, en vue d'obtenir un visage ou non. Source: F. Zapata
Tableau de distribution de probabilité discrets qui suit le lancement de deux devises honnêtes, en vue d'obtenir un visage ou non. Source: F. Zapata Variables avec distribution uniforme
-La sélection d'un nombre entier qui est uniforme ou impair: chacune est une probabilité égale à ½ d'être choisi dans l'ensemble des nombres entiers.
-Le lancement d'un dés honnête. Dans ce cas, il y a 6 faces numérotées et chacune a la même probabilité de partir: 1/6.
-La sélection d'un sujet à passer un examen, choisi entre les problèmes, si tous sont tout aussi probables.
Variables avec distribution binomiale
-Nombre de visages qui sortent en lançant une pièce honnête.
-D'une population de 250 familles, le nombre de ceux qui ont 2 enfants.
-La quantité de bois de rose qui survivent, après un jardinier 20 Rosales dans un jardin.
-D'une étude avec 50 patients, le nombre d'entre eux qui ont présenté une réaction négative à un médicament.
-Le nombre d'étudiants approuvés dans un examen de probabilités, d'un groupe composé de 100 étudiants.
Variables avec la distribution de Poisson
-Nombre d'appels par minute à Centre d'appel D'une entreprise.
-Nombre de grands tremblements de terre par an pour une zone géographique spécifique.
-Le nombre de tornades qui ont affecté une certaine région au cours de la dernière année.
-Nombre d'arbres infectés par un champignon, par hectare carré de forêt.
Variables avec distribution hypergéométrique
-Succès de chiffres ou de combinaisons gagnantes dans le jeu.
Peut vous servir: vecteurs simultanés: caractéristiques, exemples et exercices-Sélection d'un certain nombre de femmes ou de mâles dans un échantillon de n poissons d'un bocal à poisson.
Exercices résolus
Exercice 1
Une étude a déterminé qu'en sélectionnant au hasard les adultes qui ont des smartphones, 54% d'entre eux les utilisent en classe ou en réunions. Vous souhaitez trouver la probabilité que, sélectionnant au hasard 8 personnes avec un smartphone, exactement 6 d'entre eux les utilisent en classe ou en réunions.
Solution
Cette expérience est d'accord avec une expérience binomiale, car le résultat est binaire: une personne prend le téléphone en classe ou ne le retire pas. Le fait que la personne utilise le téléphone en classe peut être appelé succès, et un échec si ce n'est pas le cas (avant qu'il ne soit expliqué que ce choix est complètement arbitraire).
Dans ce cas: p = 0.54 et q = 1- 0.54 = 0.46.
Étant donné que 8 personnes sont sélectionnées au hasard, alors n = 8 et la valeur de x est de 6, par conséquent, les valeurs nécessaires sont disponibles pour les remplacer dans la formule de distribution binomiale:
Exercice 2
Au cours d'une année récente, une clinique a enregistré 4221 naissances. Avec ces données uniques, déterminez la probabilité qu'il y ait 15 naissances en 1 jour. Cet événement est-il rare?
Solution
La distribution de Poisson est utilisée, car il est demandé pour déterminer la probabilité d'occurrence d'un événement qui se produit dans un intervalle de temps. Dans ce cas, la variable est la quantité de naissances et l'intervalle est 1 jour.
La formule de distribution de Poisson nécessite la naissance moyenne par jour, qui est facilement calculée:
Par conséquent, la probabilité de x = 15 naissances / jour est:
Le résultat peut être exprimé en termes de pourcentage de clarté: 6.42% probable que, n'importe quel jour, exactement 15 naissances se produisent. L'événement est peu probable, bien qu'en aucun cas impossible.


=\frac1n)
=\fracn!\left&space;(&space;n-x&space;\right&space;)!\cdot&space;x!\cdot\:p^x\cdot&space;q^n-x)
=\frac\mu&space;^x\cdot&space;e^-\mu&space;x!)
=\fracA!\left&space;(A-x&space;\right&space;)!\cdot&space;x!\cdot&space;\fracB!\left&space;(B-n+x&space;\right&space;)!\cdot&space;\left&space;(n-x&space;\right&space;)!\div&space;\frac\left&space;(A+B&space;\right&space;)!\left&space;(A+B-n&space;\right&space;)!\cdot&space;n!)
=\frac8!\left&space;(8-6&space;\right&space;)!\times&space;6!\times&space;0.54^6\times&space;0.46^\left&space;(8-6&space;\right&space;)=\frac8!2!\times&space;6!\times&space;0.54^6\times&space;0.46^2=0.147)

=\frac11.56^15\times&space;e^-11.5615!=0.0642)