Distribution de formule normale, caractéristiques, exemple, exercice

La distribution normale o La distribution gaussienne est la distribution de probabilité en variable continue, dans laquelle la fonction de densité de probabilité est décrite par une fonction exponentielle de l'argument quadratique et négatif, ce qui se traduit par une forme ébréchante.

Le nom de distribution normal provient du fait que cette distribution est celle qui est appliquée au plus grand nombre de situations où une variable aléatoire continue est impliquée dans un groupe ou une population donnée.

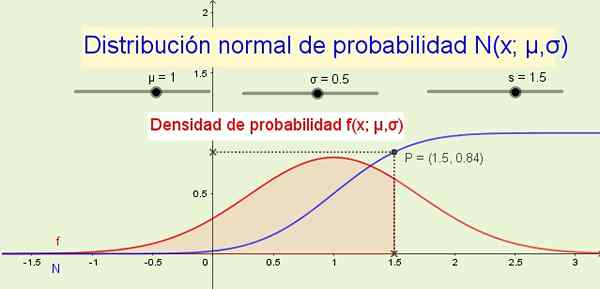
Figure 1. Distribution normale n (x; μ, σ) et sa densité de probabilité f (s; μ, σ). (Élaboration propre)

Comme exemples où une distribution normale est appliquée: la hauteur des hommes ou des femmes, des variations à l'étendue d'une grande ampleur ou dans des caractéristiques psychologiques ou sociologiques mesurables telles que le quotient intellectuel ou les habitudes de consommation d'un certain produit.

D'un autre côté, il s'appelle Gaussien Distribution ou Gauss Bell, car c'est ce génie mathématique allemand qui est crédité de sa découverte pour l'usage qu'il a donné pour la description de l'erreur statistique des mesures astronomiques en 1800 en 1800.

Cependant, il est affirmé que cette distribution statistique a déjà été publiée par un autre grand mathématicien d'origine française, tout comme Abraham de Moivre, en 1733.

[TOC]

Formule

À la fonction de distribution normale dans la variable continue X, Avec des paramètres μ et σ Il est indiqué par:

N (x; μ, σ)

Et explicitement, il est écrit comme ceci:

N (x; μ, σ) = ∫_-∞^X f (s; μ, σ) ds

où f (u; μ, σ) C'est la fonction de densité de probabilité:

f (s; μ, σ) = (1 / (σ√ (2π)) exp (- s²/ (2σ²)

La constante qui multiplie la fonction exponentielle dans la fonction de densité de probabilité est appelée constante de normalisation, et a été choisie de telle manière que:

N (+ ∞, μ, σ) = 1

L'expression précédente garantit que la probabilité que la variable aléatoire X être entre -∞ et + ∞ soit 1, c'est-à-dire une probabilité à 100%.

Le paramètre μ C'est la moyenne arithmétique de la variable aléatoire continue x et σ L'écart type ou la racine carrée de la variance de cette même variable. Dans le cas que μ = 0 et σ = 1 Vous avez la distribution de distribution standard ou normale typique: 

N (x; μ = 0, σ = 1)

Caractéristiques de distribution normales

1- Si une variable statistique aléatoire suit une distribution de densité de probabilité normale f (s; μ, σ), La plupart des données sont regroupées autour de la valeur moyenne μ Et ils sont dispersés autour d'eux afin que le peu les données soient entre μ - σ et μ + σ. 

Peut vous servir: Fréquence absolue: formule, calcul, distribution, exemple

2- L'écart type σ C'est toujours positif.

3- la forme de la fonction de densité F Il ressemble à celui d'une cloche, donc cette fonction est souvent appelée cloche gaussienne ou fonction gaussienne. 

4- Dans une distribution gaussienne, la moyenne, la médiane et la mode coïncident.

5- Les points d'inflexion de la fonction de densité de probabilité se trouvent précisément dans μ - σ et μ + σ.

6- La fonction F est symétrique par rapport à un axe qui passe par sa valeur moyenne μ Et vous n'avez aucun asymptotiquement pour x ⟶ + ∞ et x ⟶ -∞.

7- Une valeur plus élevée de σ Des données de dispersion, de bruit ou de distanciation plus importantes autour de la valeur moyenne. C'est-à-dire à plus grand σ La forme de la cloche est plus ouverte. En échange σ Small indique que les dés ont nagés à la moyenne et la forme de la cloche est plus fermée ou pointue.

8- La fonction de distribution N (x; μ, σ) indique la probabilité que la variable aléatoire soit inférieure ou égale à X. Par exemple, dans la figure 1 (ci-dessus), la probabilité p que la variable X est inférieur ou égal à 1.5 est 84% et correspond à la zone sous la fonction de densité de probabilité f (x; μ, σ) De -∞ à X.

Faire des intervalles de confiance

9- Si les données suivent une distribution normale, alors 68,26% d'entre eux sont entre μ - σ et μ + σ.

10 à 95,44% des données qui suivent une distribution normale sont entre μ - 2σ et μ + 2σ.

11- 99,74% des données qui suivent une distribution normale sont entre μ - 3σ et μ + 3σ.

12- Si une variable aléatoire X Suivre une distribution N (x; μ, σ), Puis la variable

Z = (x - μ) / σ  Suivez la distribution normale standard  N (z; 0,1).

Le changement de la variable X aile z Il est appelé standardisation ou typographie et est très utile au moment de l'application des tables de distribution standard aux données qui suivent une distribution normale non standard.

Applications de distribution normales

Pour appliquer la distribution normale, il est nécessaire de passer par le calcul de l'intégrale de la densité de probabilité, qui du point de vue analytique n'est pas facile et n'est pas toujours disponible un programme informatique qui permet son calcul numérique. À cette fin, les tableaux de valeurs standard ou typifiés sont utilisés, ce qui n'est rien de plus que la distribution normale dans le cas μ = 0 et σ = 1.

Peut vous servir: opérations combinées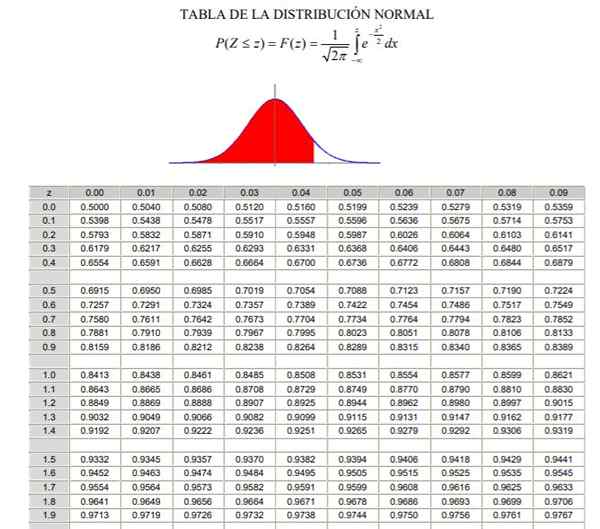Tableau de distribution normal caractérisé (partie 1/2) 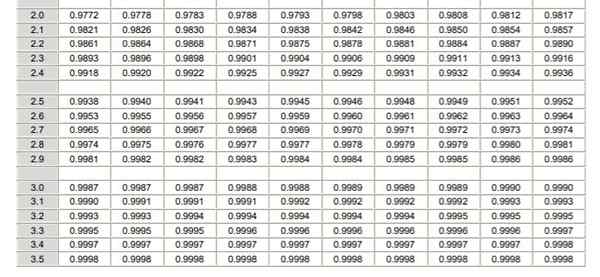Tableau de distribution normal caractérisé (partie 2/2)

Il convient de noter que ces tableaux n'incluent pas les valeurs négatives. Cependant, en utilisant les propriétés de symétrie de la fonction de densité de probabilité gaussienne, les valeurs correspondantes peuvent être obtenues. Dans l'exercice résolu illustré ci-dessous, l'utilisation du tableau est indiquée dans ces cas.

Exemple

Supposons que vous avez un ensemble de données aléatoires X qui suivent une distribution moyenne normale de 10 et l'écart type 2. Il est demandé de trouver la probabilité que:

a) La variable aléatoire x est inférieure ou égale à 8.

b) est inférieur ou égal à 10.

c) Cette variable x est inférieure à 12.

d) La probabilité qu'une valeur x se situe entre 8 et 12.

Solution:

a) Pour répondre à la première question que vous n'avez qu'à calculer:

N (x; μ, σ)

Avec x = 8, μ = 10 et σ = 2. Nous réalisons que c'est une intégrale qui n'a pas de solution analytique dans les fonctions élémentaires, mais la solution est exprimée en fonction de la fonction d'erreur Erf (x).

D'un autre côté, il est possible de résoudre l'intégrale de manière numérique, ce que de nombreux calculatrices, feuilles de calcul et programmes informatiques tels que Geogebra font. La figure suivante montre la solution numérique correspondant au premier cas:

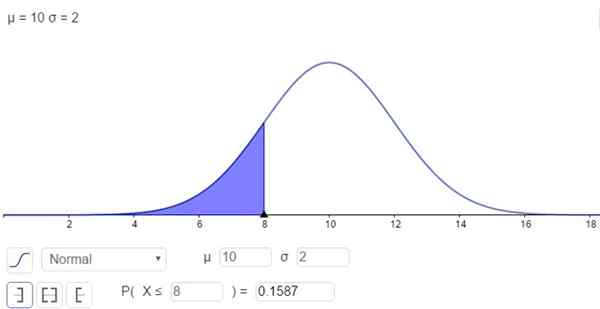Figure 2. Densité de probabilité f (x; μ, σ). La zone ombrée représente P (x ≤ 8). (Élaboration propre)

Et la réponse est que la probabilité que X soit inférieure à 8 est:

P (x ≤ 8) = n (x = 8; μ = 10, σ = 2) = 0,1587

b) Dans ce cas, il s'agit de trouver la probabilité que la variable aléatoire x soit inférieure à la moyenne que dans ce cas vaut 10. La réponse ne nécessite aucun calcul, car nous savons que la moitié des données sont inférieures à la moyenne et l'autre moitié supérieure à la moyenne. Par conséquent, la réponse est:

P (x ≤ 10) = n (x = 10; μ = 10, σ = 2) = 0,5

c) Pour répondre à cette question, vous devez calculer N (x = 12; μ = 10, σ = 2), ce qui peut être fait avec une calculatrice qui a des fonctions statistiques ou par des logiciels tels que Geogebra:

Peut vous servir: Diviseurs de 8: Quelles sont les explications faciles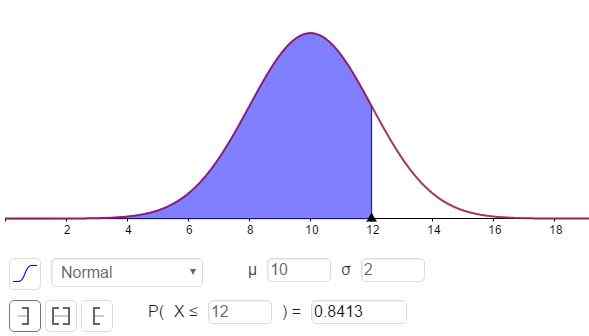figure 3. Densité de probabilité f (x; μ, σ). La zone ombrée représente P (x ≤ 12). (Élaboration propre)

La réponse à la partie C peut être vue dans la figure 3 et est:

P (x ≤ 12) = n (x = 12; μ = 10, σ = 2) = 0,8413.

d) Pour trouver la probabilité que la variable aléatoire x se situe entre 8 et 12, nous pouvons utiliser les résultats des parties A et C comme suit:

P (8 ≤ x ≤ 12) = p (x ≤ 12) - p (x ≤ 8) = 0,8413 - 0,1587 = 0,6826 = 68,26.

Exercice résolu

Le prix moyen des actions d'une entreprise est de 25 $ avec un écart-type de 4 $. Déterminez la probabilité que:

a) Une action a un coût inférieur à 20 $.

b) qui a un coût supérieur à 30 $.

c) Le prix se situe entre 20 $ et 30 $.

Utilisez les tables de distribution normales typifiées pour trouver les réponses.

Solution:

Afin d'utiliser les tables, il est nécessaire de se déplacer vers la variable normalisée ou caractérisée:

20 $ dans la variable standardisée égaux Z = (20 $ - 25 $) / 4 $ = -5/4 = -1,25 et 

30 $ dans la variable standardisée égaux z = (30 $ - 25 $) / 4 $ = +5/4 = +1,25.

a) 20 $ équivaut à -1,25 dans la variable standardisée, mais le tableau n'a pas de valeurs négatives, nous plaçons donc la valeur +1,25 qui montre la valeur de 0,8944.

Si cette valeur est soustraite 0,5, le résultat sera la zone entre 0 et 1,25 qui, soit dit en passant, est identique (par symétrie) à la zone entre -1.25 et 0. Le résultat de la soustraction est de 0,8944 - 0,5 = 0,3944, ce qui est la zone entre -1.25 et 0.

Mais la zone intéresse de -∞ à -1,25 qui sera de 0,5 à0,3944 = 0,1056. Il est donc conclu que la probabilité qu'une action soit inférieure à 20 $ est de 10,56%.

b) 30 $ dans la variable typiquement z est 1,25. Pour cette valeur dans le tableau apparaît le nombre de 0,8944 qui correspond à la zone de -∞ à +1,25. La zone entre +1.25 y + ∞ est (1 - 0,8944) = 0,1056. En d'autres termes, la probabilité qu'une action coûte plus de 30 $ est de 10,56%.

c) La probabilité qu'une action ait un coût entre 20 $ et 30 $ sera calculée comme suit:

100% -10,56% - 10,56% = 78,88%

Les références

1. Statistique et probabilité. Distribution normale. Récupéré de: projectoScartes.org
2. Géogebra. Geogebra classique, calcul de probabilité. Récupéré de Geogebra.org
3. Mathématiques. Distribution de Gauss. Récupéré de: est.Mathématiques.com
4. Mendenhall, w. 1981. Statistiques pour l'administration et l'économie. 3e. édition. Groupe éditorial IberoAmerica.
5. Trek des statistiques. Apprenez-vous des statistiques. Distribution de Poisson. Récupéré de: StatTrek.com,
6. Triola, m. 2012. Statistiques élémentaires. 11ème. Élégant. Pearson Education.
7. Université de Vigo. Principales distributions continues. Récupéré de: anapg.sites Internet.Uvigo.est
8. Wikipédia. Distribution normale. Récupéré de: est.Wikipédia.org