Formules de distribution de Poisson, équations, modèle, propriétés

La Distribution de Poisson Il s'agit d'une distribution de probabilités discrètes, à travers laquelle vous pouvez connaître la probabilité que, dans un grand échantillon et pendant un certain intervalle, un événement dont la probabilité est petite se produit.

Souvent, la distribution de Poisson peut être utilisée à la place de la distribution binomiale, tant que les conditions suivantes décrites sont atteints: grand échantillon et faible probabilité.

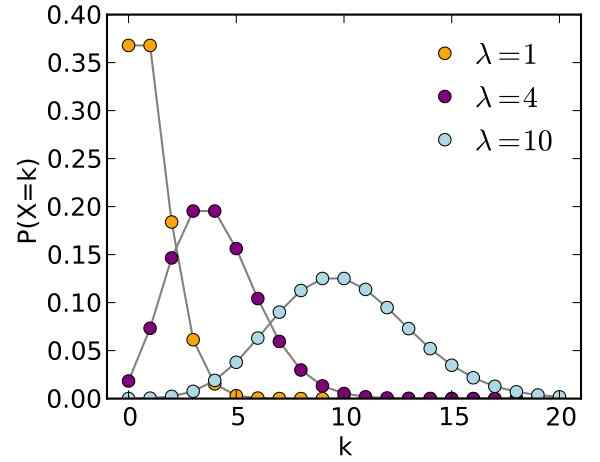
Figure 1. Graphique de distribution de Poisson pour différents paramètres. Source: Wikimedia Commons.

Siméon-denis Poisson (1781-1840) a créé cette distribution qui porte son nom, très utile en ce qui concerne les événements imprévisibles. Poisson a publié ses résultats en 1837, un travail de recherche sur la probabilité d'occurrence de peines criminelles erronées.

Par la suite, d'autres chercheurs ont adapté la distribution dans d'autres domaines, par exemple, le nombre d'étoiles qui pourraient être dans un certain volume d'espace, ou la probabilité qu'un soldat meure à cause du coz d'un cheval.

[TOC]

Formule et équations

La forme mathématique de la distribution de Poisson est la suivante:

 - La variable aléatoire est et

- μ (aussi parfois indiqué λ) C'est le paramètre moyen ou de distribution

- Numéro d'Euler: E = 2.71828

- La probabilité d'obtenir y = k est p

- k C'est le nombre de succès 0, 1,2,3 ..

- n C'est le nombre de tests ou d'événements (taille de l'échantillon)

Les variables aléatoires discrètes, comme son nom l'indique, dépendent du hasard et ne prennent que des valeurs discrètes: 0, 1, 2, 3, 4 ..., k.

La moyenne de la distribution est donnée par:

La variance σ, qui mesure la dispersion des données, est un autre paramètre important. Pour la distribution de Poisson, c'est:

σ = μ

Poisson a déterminé que lorsque N → ∞ et P → 0, la moyenne μ -So appelée valeur attendue- Il tend à une constante:

μ → constant

Important: p C'est la probabilité d'occurrence de l'événement qui tient compte de la population totale, tandis que P (y) C'est la prédiction de Poisson sur l'échantillon.

Modèle et propriétés

La distribution de Poisson a les propriétés suivantes:

-La taille de l'échantillon est grande: N → ∞.

-Les événements ou événements considérés sont indépendants les uns des autres et se produisent au hasard.

-Probabilité P Quel certain événement et Il se produit pendant une période de temps spécifique est très faible: P → 0.

-La probabilité de plus d'un événement dans l'intervalle de temps est 0.

-La valeur moyenne est proche d'une constante donnée par: μ = n.P (n est la taille de l'échantillon)

-Étant donné que la dispersion σ est égale à μ, car elle adopte des valeurs plus élevées, la variabilité est également plus élevée.

-Les événements doivent être répartis uniformément dans l'intervalle de temps utilisé.

-L'ensemble des valeurs d'événements possibles et C'est: 0,1,2,3,4 .. .

Peut vous servir: Expérience aléatoire: concept, espace d'échantillonnage, exemples

-La somme de Toi Les variables qui suivent une distribution de Poisson, est également une autre variable de Poisson. Sa valeur moyenne est la somme des valeurs moyennes de ces variables.

Différences avec la distribution binomiale

La distribution de Poisson diffère de la distribution binomiale dans les aspects importants suivants:

-La distribution binomiale est affectée à la fois par la taille de l'échantillon S et par la probabilité P, Mais la distribution de Poisson n'est affectée que par la moyenne μ.

-Dans une distribution binomiale, les valeurs possibles de la variable aléatoire et Ils sont de 0,1,2,…, à la place dans la distribution de Poisson, il n'y a pas de limite supérieure pour ces valeurs.

Exemples

Poisson a initialement appliqué sa célèbre distribution aux affaires juridiques, mais au niveau industriel, l'une de ses premières utilisations a été dans la fabrication de la bière. Dans ce processus, les cultures de levure sont utilisées pour la fermentation.

La levure est constituée de cellules vivantes, dont la population est variable dans le temps. Dans la fabrication de la bière, il est nécessaire d'ajouter la quantité nécessaire, il est donc nécessaire de connaître la quantité de cellules par unité de volume.

Pendant la Seconde Guerre mondiale, la distribution de Poisson a été utilisée pour savoir si les Allemands pointent vraiment vers Londres de Calais, ou simplement tirant au hasard. C'était important pour les Alliés de déterminer à quel point il était bon la technologie disponible pour les nazis.

Applications pratiques

Les applications de distribution de Poisson se réfèrent toujours au nombre de temps ou à des dénombrements d'espace. Et comme la probabilité d'occurrence est petite, elle est également connue sous le nom de "loi d'événements rares".

Voici une liste d'événements qui tombent dans l'une de ces catégories:

-L'enregistrement des particules dans une décroissance radioactive, qui, comme la croissance des cellules de levure, est une fonction exponentielle.

-Nombre de visites sur un certain site Web.

-Arrivée de personnes à une rangée pour payer ou être assistée (théorie des queues).

-Nombre de voitures qui traversent un certain point sur une route, pour un intervalle de temps donné.

Figure 2. La quantité de voitures qui passe par un point suit approximativement une distribution de Poisson. Source: Pixabay.

-Mutations subies dans une certaine chaîne d'ADN après avoir reçu une exposition au rayonnement.

-Nombre de météores de diamètre supérieur à 1 m tombé en un an.

-Défauts par mètre carré d'un tissu.

-Quantité de cellules sanguines dans 1 centimètre cube.

-Appels par minute à un échange téléphonique.

-Des étincelles de chocolat présentent dans 1 kg de pâte à gâteau.

-Nombre d'arbres infectés par le chemin dans 1 hectare de forêt.

Notez que ces variables aléatoires représentent le nombre de fois qu'un événement se produit pendant une période fixe (Appels par minute à l'échange téléphonique), ou une région d'espace donnée (Défauts d'un tissu par mètre carré).

Peut vous servir: variation proportionnelle

Ces événements, comme déjà établis, sont indépendants du temps qui s'est écoulé depuis la dernière occurrence.

Approchant la distribution binomiale avec la distribution de Poisson

La distribution de Poisson est une bonne approche de la distribution binomiale tant que:

-La taille de l'échantillon est grande: n ≥ 100

-Probabilité p est petite: P ≤ 0,1

- μ être dans l'ordre de: Np ≤ 10

Dans de tels cas, la distribution de Poisson est un excellent outil, car la distribution binomiale peut devenir compliquée à appliquer dans ces cas.

Exercices résolus

Exercice 1

Une étude sismologique a déterminé qu'au cours des 100 dernières années, il y avait 93 grands tremblements de terre dans le monde, au moins 6.0 sur l'échelle Richter -Logarithmic-. Supposons que la distribution de Poisson soit un modèle adéquat dans ce cas. Trouver:

a) L'occurrence moyenne de grands tremblements de terre par an.

b) Oui P (y) C'est la probabilité de se produire et Treatoires pour une année sélectionnée aléatoire, trouvez les probabilités suivantes:

P(0), P(1), P (2), P (3), P (4), P (5), P (6) et P (7).

c) Les vrais résultats de l'étude sont les suivants:

- 47 ans (0 tremblements de terre)

- 31 ans (1 tremblements de terre)

- 13 ans (2 tremblements de terre)

- 5 ans (3 tremblements de terre)

- 2 ans (4 tremblements de terre)

-  0 ans (5 tremblements de terre)

- 1 ans (6 tremblements de terre)

- 1 ans (7 tremblements de terre)

Comment ces résultats sont-ils obtenus dans le paragraphe B? La distribution de Poisson est-elle un bon choix pour modéliser ces événements?

Solution à)

a) Les tremblements de terre sont des événements dont la probabilité p Il est petit et nous envisageons une période de temps restreinte, d'un an. Les tremblements de terre moyens sont:

μ = 93/100 Trewkeakes / an = 0.93 tremblements de terre par an.

Solution b)

b) Pour calculer les probabilités demandées, les valeurs sont remplacées dans la formule donnée au début:

Par exemple pour trouver P (2), ce qui serait la probabilité qu'il y aura 2 grands tremblements de terre par an:

y = 2

μ = 0.93

E = 2.71828

Et c'est la probabilité qu'il y ait 7 grands tremblements de terre pendant un an:

C'est assez inférieur à P (2).

Les résultats sont répertoriés ci-dessous:

P (0) = 0.395, p (1) = 0.367, p (2) = 0.171, p (3) = 0.0529, p (4) = 0.0123, p (5) = 0.00229, p (6) = 0.000355, p (7) = 0.0000471.

Par exemple, nous pourrions dire qu'il y a une probabilité de 39.5% qu'aucun grand tremblement de terre ne se produit au cours d'une année donnée. Ou qu'il y a 5,29% que 3 grands tremblements de terre se produisent cette année-là.

Solution C)

c) Les fréquences sont analysées, multipliant par n = 100 ans:

39.5; 36.7; 17.1 ; 5.29; 1.23 0.229; 0.0355 et 0.00471.

Peut vous servir: dérivés algébriques

Par exemple:

- Une fréquence de 39.5 indique que, en 39.5 des 100 ans ou de grands tremblements de terre se produisent, nous pourrions dire qu'il est assez proche du vrai résultat de 47 ans sans aucun grand tremblement de terre.

Comparons un autre résultat de Poisson avec des résultats réels:

- La valeur obtenue à partir de 36.7 signifie que dans une période de 37 ans, il y a 1 grand tremblement de terre. Le vrai résultat est qu'en 31 ans, il y a eu 1 grand tremblement de terre, une bonne coïncidence avec le modèle.

- 17 sont attendus.1 ans avec 2 grands tremblements de terre et il est connu qu'en 13 ans, ce qui est une valeur rapprochée, il y avait en effet 2 grands tremblements de terre.

Par conséquent, le modèle de Poisson est acceptable pour cette affaire.

Exercice 2

Une entreprise estime que le nombre de composants qui échouent avant de terminer 100 heures de fonctionnement, suit une distribution de Poisson. Si le nombre moyen de défaillances est de 8 à ce moment-là, trouvez les probabilités suivantes:

a) qu'un composant échoue en 25 heures.

b) échec moins de deux composants, en 50 heures.

c) qu'au moins trois composants échouent en 125 heures.

Solution à)

a) Il est connu que la faute moyenne en 100 heures est de 8, donc en 25 heures, la quatrième partie des échecs est attendue, c'est-à-dire 2 échecs. Ce sera le paramètre μ.

La probabilité d'échec de 1 composant est demandée, la variable aléatoire est «les composants qui échouent avant 25 heures» et sa valeur est y = 1. En remplaçant dans la fonction de probabilité:

 b) Maintenant, la variable aléatoire est "des composants qui échouent avant 50 heures". Le paramètre est μ = 4, Puisque la valeur attendue des échecs en 50 heures est 4.

Cependant, la question est la probabilité que moins de deux composants échouent en 50 heures, et non exactement que 2 composants échouent en 50 heures, nous devons donc ajouter les probabilités qui:

-Aucun échoue

-Échouer seulement 1

P (moins de 2 composants) = P (0) + P (1)

P (moins de 2 composants) = 0.0183 + 0.0732 = 0.0915

c) qu'au moins 3 composants échouent en 125, cela signifie que 3, 4, 5 ou plus à ce moment-là peuvent échouer.

La probabilité qui se produit au moins un des plusieurs événements est égale à 1, sauf la probabilité qu'aucun des événements ne se produise.

-L'événement recherché est d'échouer 3 composants ou plus en 125 heures

-Le fait que l'événement ne se produise pas signifie que moins de 3 composants échouent, dont la probabilité est: P (0) + P (1) + P (2)

Le paramètre μ de la distribution dans ce cas est:

 μ = 8 + 2 = 10 échecs en 125 heures.

P (Fallen 3 ou plus composants) = 1- P (0) - P (1) - P (2) =

= 1-0.0026786 = 0.9972

Les références

1. Mathématiques. Distribution de Poisson. Récupéré de: est.Mathématiques.com
2. Mendenhall, w. 1981. Statistiques pour l'administration et l'économie. 3e. édition. Groupe éditorial IberoAmerica.
3. Trek des statistiques. Apprenez-vous des statistiques. Distribution de Poisson. Récupéré de: StatTrek.com,
4. Triola, m. 2012. Statistiques élémentaires. 11ème. Élégant. Pearson Education.
5. Wikipédia. Distribution de Poisson. Récupéré de: dans.Wikipédia.org