Concept de distance euclidienne, formule, calcul, exemple

La Distance euclidienne C'est un nombre positif qui indique la séparation que deux points ont dans un espace où les axiomes et les théorèmes de la géométrie euclide sont respectés.

La distance entre deux points A et B d'un espace euclidien est la longueur du vecteur UN B Appartenant à la seule ligne qui passe par ces points.

Figure 1 . Espace euclidien unidimensionnel formé par la ligne (OX). Plusieurs points sur cet espace, leurs coordonnées et leurs distances sont affichées. (Préparé par Ricardo Pérez).

L'espace que nous percevons et où nous déplaçons les êtres humains est un espace tridimensionnel (3-D), où les axiomes et les théorèmes de la géométrie des eucléides sont remplis. Dans cet espace, il y a des sous-espaces à deux dimensions (plans) et des sous-espaces de dimension (droite) (droits).

Les espaces euclidiens peuvent être d'une dimension (1-d), de deux dimensions (2-D), de trois dimensions (3-D) ou des dimensions N (N-D).

Ce sont des points dans l'espace d'une seule dimension x qui appartient à la ligne orientée (OX), la direction de ou à x est l'adresse positive. Pour localiser les points sur cette ligne, le système cartésien qui consiste à attribuer chaque point de la ligne est utilisé un nombre.

[TOC]

Formule

La distance euclidienne d (a, b) est définie entre les points A et B, située sur une ligne, comme la racine carrée du carré des différences de ses coordonnées x:

D (a, b) = √ ((xb - xa) ^ 2)

Cette définition garantit que: la distance entre deux points est toujours un montant positif. Et que la distance entre a et b est égale à la distance entre b et a.

La figure 1 montre l'espace euclidien d'une seule dimension formé par la ligne (OX) et plusieurs points sur cette ligne. Chaque point a une coordonnée:

Le point A a une coordonnée xa = 2.5, la coordonnée B xb = 4 et le point C coordonnée xc = -2.5

Il peut vous servir: Probabilité de fréquence: concept, comment il est calculé et des exemples

D (a, b) = √ ((4 - 2.5) 2) = 1.5

D (b, a) = √ ((2.5 - 4) 2) = 1.5

D (a, c) = √ ((-2.5 - 2.5) 2) = 5.0

Distance euclidienne en deux dimensions

L'espace d'euclides à deux dimensions est un plan. Les points d'un plan euclidien rencontrent les axiomes de la géométrie euclide, par exemple:

- Sur deux points une seule ligne passe. 

- Trois points sur l'avion forment un triangle dont les angles internes ajoutent toujours 180º.

- Dans un triangle rectangulaire, le carré de l'hypoténuse est égal à la somme des carrés de ses jambes.

En deux dimensions, un point a des coordonnées x et y. 

Par exemple, un point P a des coordonnées (XP, YP) ​​et un point coordonné (XQ, YQ).

La distance euclidienne entre le point P et le Q est définie avec la formule suivante:

D (p, q) = √ ((xq - xp) ^ 2 + (yq - yp) ^ 2)

Il convient de noter que cette formule est équivalente au théorème de Pythagore, comme le montre la figure 2.

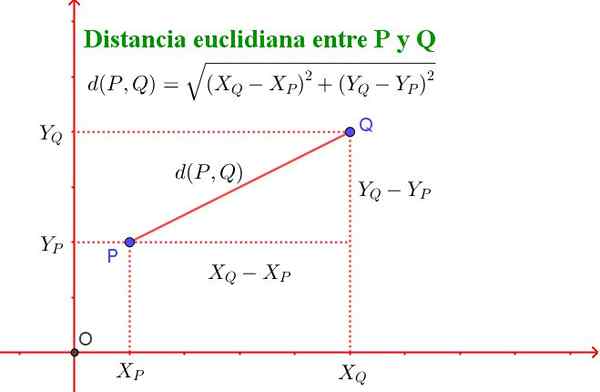Figure 2. La distance entre deux points P et Q de l'avion rencontre le théorème de Pythagore. (Préparé par Ricardo Pérez).

Surfaces non pécudiennes

Tous les espaces de dimension ne rencontrent pas la géométrie euclidienne. La surface d'une sphère est un espace à deux dimensions.

Les angles d'un triangle sur une surface sphérique n'ajoutent pas 180 ° et avec cela, le théorème de Pythagore n'est pas rempli, donc une surface sphérique ne remplit pas les axiomes d'Euclide.

Distance euclidienne en n dimensions

Le concept de coordonnées peut être étendu à de plus grandes dimensions:

- Dans le point 2D, P a des coordonnées (XP, YP)

- En 3-D un point qui a des coordonnées (XQ, YQ, ZQ)

- Dans 4D Point R aura des coordonnées (XR, YR, ZR, WR)

- Dans N-D, un point P aura des coordonnées (P1, P2, P3, ..., PN)

Peut vous servir: Bars Graph: Caractéristiques, à quoi sert, des exemples

La distance entre deux points p et q d'un espace euclidien à n dimensions est calculée avec la formule suivante:

D (p, q) = √ ((q1 - p1) ^ 2 + (q2 - p2) ^ 2 +… + (qn - pn) ^ 2)

Le lieu géométrique de tous les points qui, dans un espace euclidien à n dimensions, qui équivaut à un autre point P fixe (le centre) forment une hypersféra à n dimensions.

Comment calculer la distance euclidienne

Ci-dessous, la distance entre deux points située dans l'espace euclidien à trois dimensions est calculé.

Supposons le point A des coordonnées cartésiennes x, y, z données par a :( 2, 3, 1) et le point B des coordonnées b :( -3, 2, 2).

Vous souhaitez déterminer la distance entre ces points, pour laquelle la relation générale est utilisée:

D (a, b) = √ ((-3 - 2) 2 + (2 - 3) 2 + (2 - 1) 2) = √ ((-5) 2 + (-1) 2 + (1) 2 )

D (a, b) = √ (25 + 1 + 1) = √ (27) = √ (9 * 3) = 3 √ (3) = 5,196

Exemple

Il y a deux points P et Q.  Le point P pour les coordonnées cartésiennes x, y, z données par p :( 2, 3, 1) et le point Q des coordonnées Q :( -3, 2, 1).

Il est invité à trouver les coordonnées du point médian M du segment [PQ] qui relie les deux points. 

Solution:

On suppose que le point inconnu M a des coordonnées (x, y, z).

Comme m est le point moyen de [pq], il doit être accompli que d (p, m) = d (q, m), il doit également être rempli d (p, m) ^ 2 = d (q, m) ^ 2:

(X - 2) ^ 2 + (y - 3) ^ 2 + (z - 1) ^ 2 = (x - (-3)) ^ 2 + (y - 2) ^ 2 + (z - 1) ^ 2

Comme dans ce cas, le troisième terme est le même dans les deux membres où l'expression précédente est simplifiée:

Peut vous servir: constante absolue

(X - 2) ^ 2 + (y - 3) ^ 2 = (x + 3) ^ 2 + (y - 2) ^ 2 

Il y a alors une équation avec deux inconnues x et y. Une autre équation est nécessaire pour résoudre le problème.

Le point M appartient à la ligne qui passe par les points P et Q, que nous pouvons calculer comme suit:

Le premier est le réalisateur Vector Pq de la ligne: Pq = = .

Alors P.m = Faire un coup de pouce + pour Pq, où Faire un coup de pouce C'est la position vectorielle du point p et pour C'est un paramètre qui appartient à des nombres réels. 

L'équation précédente est connue sous le nom d'équation vectorielle de la ligne, qui dans les coordonnées cartésiennes adopte comme suit:

= + a =

Égal les composants correspondants sont:

X - 2 = 2 - 5 a; Et - 3 = 3 -A; Z - 1 = 0

C'est-à-dire que x = 4 - 5a, y = 6 - a, enfin z = 1.

Il est remplacé dans l'expression quadratique qui relie x à y:

(4 - 5a - 2) ^ 2 + (6 - a - 3) ^ 2 = (4 - 5a + 3) ^ 2 + (6 - a - 2) ^ 2

Il est simplifié:

(2 - 5a) ^ 2 + (3 -a) ^ 2 = (7 - 5a) ^ 2 + (4 - a) ^ 2

Se développe maintenant:

4 + 25 a ^ 2 - 20a + 9 + a ^ 2 - 6a = 49 + 25 a ^ 2 - 70a + 16 + a ^ 2 - 8a

Il est simplifié, annulant des termes similaires dans les deux membres:

4 - 20a + 9 - 6a = 49 - 70a + 16 - 8a

Paramètre A:

52 a = 49 + 16 - 4 - 9 = 52 résultant que a = 1.

C'est-à-dire que x = 4 - 5, y = 6 - 1, enfin z = 1.

Enfin, nous obtenons les coordonnées cartésiennes du point médian M du segment [PQ]:

M: (-1, 5, 1).

Les références

1. Lehmann C. (1972) Géométrie analytique. Uteha.
2. Superprof. Distance entre deux points. Récupéré de: superprof.est
3. Unam. Distance entre les variétés sous-linéaires connexes. Récupéré de: Prométhée.Matem.Unam.mx /
4. Wikipédia. Distance euclidienne. Récupéré de: est.Wikipédia.com
5. Wikipédia. Espace euclidien. Récupéré de: est.Wikipédia.com