Formule d'expansion de surface, coefficients et exemples

La dilatation superficielle C'est l'expansion qui se produit lorsqu'un objet subit des variations de sa surface en raison de la variation de la température. Il est dû aux caractéristiques du matériau ou de sa forme géométrique. La dilatation prédomine en deux dimensions dans la même proportion.

Par exemple dans une feuille, lorsqu'il y a une variation de la température, c'est la surface de la même chose qui subit le plus grand changement en raison de la dilatation thermique.

La surface d'une plaque métallique qui est généralement observée dans les rues. Source: Pixabay.

La feuille de métaux de la figure précédente augmente sa large et sa longueur appréciable lorsqu'elle est chauffée par le rayonnement solaire. Au contraire, les deux diminuent considérablement lorsqu'ils sont refroidis en raison d'une diminution de la température ambiante.

C'est pour cette raison que, lorsque les carreaux sont installés à un étage, certains bords avec d'autres ne doivent pas être touchés, mais il doit y avoir un espace de séparation appelé carton de dilatation.

De plus, cet espace est rempli d'un mélange spécial qui a un certain degré de flexibilité, empêchant les carreaux de se fissurer en raison de fortes pressions que la dilatation thermique peut produire.

[TOC]

Qu'est-ce que la dilatation superficielle?

Dans un matériau solide, les atomes maintiennent leurs positions relatives plus ou moins fixes autour d'un point d'équilibre. Cependant, en raison de l'agitation thermique, ils oscillent toujours autour.

En augmentant la température, l'oscillation thermique augmente également, provoquant le changement des positions d'oscillation moyenne. En effet.

Vous trouverez ci-dessous un chiffre qui décrit l'énergie de liaison chimique en fonction de la distance interatomique. L'énergie d'oscillation totale à deux températures est également montrée et comment le centre d'oscillation se déplace.

Il peut vous servir: Pascal Tonel: comment ça marche et expériences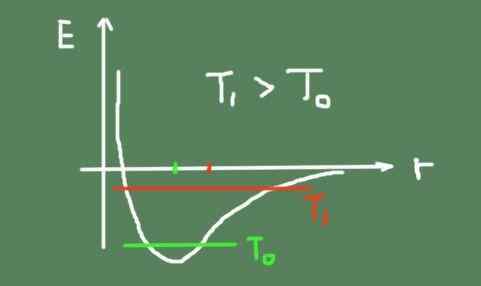Graphique énergétique du lien versus distance interatomique. Source: auto-faite.

Dilatation superficielle et son coefficient

Pour mesurer la dilatation superficielle, nous commençons à partir d'une zone initiale A et d'une température initiale t, de l'objet dont la dilatation doit être mesurée.

Supposons que cet objet soit une lame de la zone A, et son épaisseur est bien inférieure à la racine carrée de la zone A. La feuille est soumise à une variation de température ΔT, de sorte que la température finale de la même une fois que l'équilibre thermique avec la source de chaleur sera établi soit t '= t + Δt.

Au cours de ce processus thermique, la surface aura également changé à une nouvelle valeur à '= a + Δa. Ainsi, le coefficient de dilatation de surface σ est défini comme le rapport entre la variation relative de la surface par unité de variation de température.

La formule suivante définit le coefficient de dilatation superficiel σ:

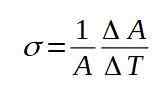
Le coefficient de dilatation superficiel σ est pratiquement constant pour une large gamme de valeurs de température.

En raison de la définition de σ, ses dimensions sont une température inverse. En tant qu'unité, il est généralement utilisé ° C^-1.

Coefficient de dilatation de surface pour divers matériaux

Ensuite, nous donnerons une liste du coefficient de dilatation superficiel pour certains matériaux et éléments. Le coefficient est calculé en pression atmosphérique normale en fonction d'une température ambiante de 25 ° C, et sa valeur est considérée comme constante dans une plage de ΔT de -10 ° C à 100 ° C.

L'unité du coefficient de dilatation superficiel sera (° C)^-1

- Acier: σ = 24 ∙ 10^-6 (° C)^-1

- Aluminium: σ = 46 ∙ 10^-6 (° C)^-1

Il peut vous servir: aimantation: moment magnétique orbital et spin, exemples

- Or: σ = 28 ∙ 10^-6 (° C)^-1

- Cuivre: σ = 34 ∙ 10^-6 (° C)^-1

- Laiton: σ = 36 ∙ 10^-6 (° C)^-1

- Fer: σ = 24 ∙ 10^-6 (° C)^-1

- Verre: σ = (14 à 18) ∙ 10^-6 (° C)^-1

- Quartz: σ = 0,8 ∙ 10^-6 (° C)^-1

- Diamant: σ = 2 ,, 4 ∙ 10^-6 (° C)^-1

- Plomb: σ = 60 ∙ 10^-6 (° C)^-1

- Bois de chêne: σ = 108 ∙ 10^-6 (° C)^-1

- PVC: σ = 104 ∙ 10^-6 (° C)^-1

- Fibre de carbone: σ = -1,6 ∙ 10^-6 (° C)^-1

- Béton: σ = (16 à 24) ∙ 10^-6 (° C)^-1

La plupart des matériaux s'étendent avec une augmentation de la température. Cependant, certains matériaux tels que la fibre de carbone répondent à l'augmentation de la température.

Exemples résolus de dilatation superficielle

Exemple 1

Une plaque en acier a des dimensions de 3m x 5m. Le matin et à l'ombre, sa température est de 14 ° C, mais à midi, le soleil le réchauffe jusqu'à 52 ° C. Trouvez la dernière zone de la plaque.

Solution

Nous partons de la définition du coefficient de dilatation superficiel:

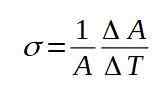
À partir d'ici, nous nettoyons la variation de la zone:

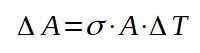
Nous procédons ensuite à remplacer les valeurs respectives pour trouver l'augmentation de la superficie avec l'augmentation de la température.

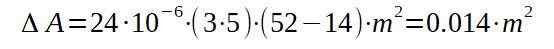
C'est-à-dire que la zone finale sera de 15 014 mètres carrés.

Exemple 2

Montrer que le coefficient de dilatation superficiel est d'environ le double du coefficient de dilatation linéaire.

Solution

Supposons que nous commencions à partir d'une plaque rectangulaire de largeur dimensions lx et longs, alors sa zone initiale sera a = lx ∙ ly

Peut vous servir: échelles thermométriques

Lorsque la plaque souffre d'une augmentation de la température ΔT, ses dimensions augmentent également étant sa nouvelle largeur lx 'et son nouveau «long, de sorte que sa nouvelle zone sera un« = lx «∙ ly»

La variation subie par la zone de la plaque en raison du changement de température sera alors

Δa = lx '∙ ly' - lx ∙ ly

où lx '= lx (1 + α Δt) et ly' = ly (1 + α Δt)

C'est-à-dire que le changement de zone en fonction du coefficient de dilatation linéaire et du changement de température sera:

Δa = lx (1 + α ΔT) ∙ ly (1 + α ΔT) - lx ∙ ly

Cela peut être réécrit comme:

Δa = lx ∙ ly ∙ (1 + α Δt) ² - lx ∙ ly

Développer le carré et le multiplication, nous avons ce qui suit:

je

Comme α est de l'ordre de 10^-6, En le soulevant carré, c'est l'ordre de 10^-12. Ainsi, le terme quadratique de l'expression précédente est méprisable.

Ensuite, l'augmentation de la zone peut être approchée par:

Δa ≈ 2α Δt lx ∙ ly

Mais l'augmentation de la superficie en fonction du coefficient de dilatation superficiel est:

Δa = γ Δt a

D'où une expression est déduite qui relie le coefficient de dilatation linéaire au coefficient de dilatation superficiel.

γ ≈ 2 ∙ α

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mac Graw Hill. 422-527
2. Giancoli, D. 2006. Physique: principes avec applications. 6e. Édition. Prentice Hall. 238-249.