Décomposition additive

La décomposition additive d'un entier positif, c'est l'exprimer comme une somme de deux ou plusieurs nombres positifs. Ainsi, nous avons ce nombre 5 peut l'exprimer comme 5 = 1 + 4, 5 = 2 + 3 ou 5 = 1 + 2 + 2. Chacune de ces façons d'écrire le numéro 5 est ce que nous appellerons la décomposition additive.

Si nous faisons attention, nous pouvons voir que les expressions 5 = 2 + 3 et 5 = 3 + 2 représentent la même composition; Les deux ont les mêmes nombres. Cependant, ce n'est que pour une question de confort.

Décomposition additive

Comme autre exemple, nous pouvons prendre le numéro 27, que nous pouvons l'exprimer comme:

27 = 7 + 10 + 10

27 = 9 + 9 + 9

27 = 3 + 6 + 9 + 9

27 = 9 + 18

La décomposition additive est un outil très utile qui nous permet de renforcer nos connaissances sur les systèmes de numérotation.

Décomposition additive canonique

Lorsque nous avons un nombre de plus de deux chiffres, une forme particulière de les décomposer est dans les multiples de 10, 100, 1000, 10 000, etc., qui se maquille. Cette façon d'écrire n'importe quel nombre est appelée décomposition additive canonique. Par exemple, le numéro 1456 peut le décomposer comme suit:

1456 = 1000 + 400+ 50 + 6

Si nous avons le numéro 20 846 295, votre décomposition additive canonique sera:

20 846 295 = 20 000 000 + 800 000 + 40 000 + 6000 + 200 + 90 +5.

Grâce à cette décomposition, nous pouvons voir que la valeur d'un chiffre donné est donnée par la position qu'il occupe. Prenons comme exemple les nombres 24 et 42:

24 = 20 + 4

42 = 40 +2

Ici, nous pouvons voir qu'en 24, le 2 a une valeur de 20 unités et sur 4 une valeur de 4 unités; D'un autre côté, en 42, le 4 a une valeur de 40 unités et les 2 des deux unités. Ainsi, bien que les deux nombres utilisent les mêmes chiffres, leurs valeurs sont totalement différentes par la position qu'ils occupent.

Peut vous servir: x au carré

Applications

L'une des applications que nous pouvons apporter à la décomposition additive est dans certains types de démonstrations, dans lesquelles il est très utile de voir un entier positif comme la somme d'autres.

Exemple de théorème

Prenons comme exemple le théorème suivant avec leurs démonstrations respectives.

- Être z un nombre entier de 4 chiffres, alors z est divisible par 5 si sa figure correspondant aux unités est nulle ou cinq.

Manifestation

Rappelons-nous ce qu'est la divisibilité. Si nous avons des nombres entiers "A" et "B", nous disons que "A" divise "B" s'il y a un entier "C" tel que b = a * c.

L'une des propriétés de la divisibilité nous dit que si "A" et "B" sont divisibles entre "C", alors la soustraction "A-B" est également.

Être z un nombre entier de 4 chiffres; Par conséquent, nous pouvons écrire à Z et Z = ABCD.

En utilisant la décomposition additive canonique, nous devons:

Z = a * 1000 + b * 100 + c * 10 + d

Il est clair que A * 1000 + B * 100 + C * 10 est divisible entre 5. C'est pourquoi nous avons que z est divisible entre 5 si z - (a * 1000 + b * 100 + c * 10) est divisible entre 5.

Mais z - (a * 1000 + b * 100 + c * 10) = d et d est un seul numéro de figure, donc la seule façon d'être divisible entre 5 est qu'elle est 0 ou 5.

Par conséquent, z est divisible entre 5 si d = 0 ou d = 5.

Notez que si z a n chiffres, la démonstration est exactement la même, cela ne change que que nous écrivions maintenant z = a₁POUR₂… POUR_n Et l'objectif serait de prouver que_n est zéro ou cinq.

Partitions

Nous disons qu'une partition d'un entier positif est une façon dont nous pouvons écrire un nombre comme une somme d'entiers positifs.

Peut vous servir: Radio de convergence: définition, exemples et exercices résolus

La différence entre une décomposition additive et une partition est que, alors que dans le premier, il est demandé qu'au moins il peut être divisé en deux ou plus, dans la partition cette restriction.

Ainsi, nous avons ce qui suit:

5 = 5

5 = 1 + 4

5 = 2 + 3

5 = 1 + 2 + 2

Ce qui précède sont des partitions de 5.

C'est-à-dire que nous avons que toute décomposition additive est une partition, mais toutes les partitions ne sont pas nécessairement une décomposition additive.

Dans la théorie des nombres, le théorème fondamental de l'arithmétique garantit que chaque nombre entier peut être écrit uniquement comme un produit de cousins.

Lorsque les partitions sont étudiées, l'objectif est de déterminer combien de façons un entier positif peut être écrit comme la somme d'autres entiers. Par conséquent, nous définissons la fonction de partition comme présenté ci-dessous.

Définition

La fonction de partition P (n) est définie comme le nombre de façons dont un entier positif n peut être écrit comme une somme d'entiers positifs.

Revenant à l'exemple de 5, nous devons:

5 = 5

5 = 1 + 4

5 = 2 + 3

5 = 1 + 1 + 3

5 = 1 + 2 + 2

5 = 1 + 1 + 1 + 2

5 = 1 + 1 + 1 + 1 + 1

De cette façon, p (5) = 7.

Graphiques

Les partitions et les décompositions additives d'un nombre n peuvent être représentées géométriquement.  Supposons que nous ayons une décomposition additive de n. Dans cette décomposition, les addeds peuvent être fixés afin que les membres de la somme soient ordonnés du moins au plus grand. Donc, ça vaut:

n = a₁ + pour₂ + pour₃ +… + A_r avec

pour₁ ≤ a₂ ≤ a₃ ≤ ... ≤ a_r.

Nous pouvons graphiquement ladite décomposition comme suit: Dans une première ligne, nous marquons le A₁-points, puis dans ce qui suit, nous marquons₂-points, et ainsi de suite jusqu'à atteindre_r.

Peut vous servir: inégalité du triangle: démonstration, exemples, exercices résolus

Prenons comme exemple numéro 23 et sa prochaine décomposition:

23 = 5 + 4 + 7 + 3 + 1 +3

Nous commandons cette décomposition et nous avons:

23 = 1 + 3 + 3 + 4+ 5 + 7

Son graphique correspondant serait:

De même, si nous lisons ce graphique verticalement à la place horizontalement, nous pouvons obtenir une décomposition qui est peut-être différente de la précédente. Dans l'exemple des 23, le suivant se démarque:

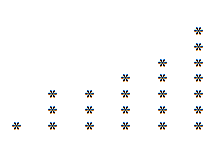
Nous avons donc cette 23 ans, nous pouvons également l'écrire comme:

23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.