Propriétés des dérivés partiels, calcul, exercices

Le dérivés partiels d'une fonction avec plusieurs variables indépendantes sont celles qui sont obtenues en prenant le dérivé ordinaire dans l'une des variables, tandis que les autres sont maintenus ou pris comme constantes.

Le dérivé partiel dans l'une des variables, détermine comment la fonction varie à chaque point, par unité de changement la variable en question. 

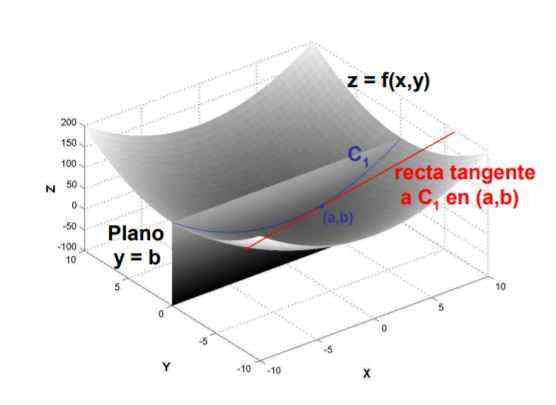Figure 1. La pente de la ligne tangente à la courbe formée par l'intersection du plan y = b avec la surface f (x, y) au point (a, b) est la dérivée partielle de f par rapport à x, évaluée à ce point. Source: UPM.est

En raison de sa définition, la dérivée partielle est calculée en prenant la limite mathématique du quotient entre la variation de la fonction et la variation de la variable par rapport à ce qui est dérivé, lorsque le changement de ce dernier tend à zéro.

Supposons le cas d'une fonction F Cela dépend des variables X et et, c'est-à-dire pour chaque paire (X, y) A est attribué z: 

f: (x, y) → z .

Le dérivé partiel de la fonction z = f (x, y), à l'égard de X est défini comme:

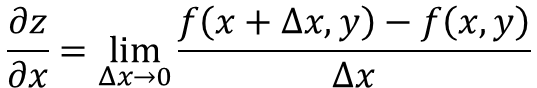
Maintenant, il existe plusieurs façons de désigner la dérivée partielle d'une fonction, par exemple:

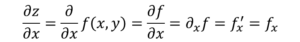
La différence avec le dérivé ordinaire, en termes de notation, est que le d de la dérivation est changée en symbole ∂, connu sous le nom de "Jacobi D".

[TOC]

Propriétés des dérivés partiels

Le dérivé partiel d'une fonction de plusieurs variables, en ce qui concerne l'un d'eux, est le dérivé ordinaire de ladite variable et considérant le reste comme fixe ou constant. Pour trouver le dérivé partiel, les règles de dérivation des dérivés ordinaires peuvent être utilisées.

Sous les principales propriétés:

Peut vous servir: facteur commun pour le regroupement des termes: exemples, exercices

Continuité

Si une fonction f (x, y) a des dérivés partiels en X et et Sur le point (Xo, moi) alors on peut dire que la fonction est continue à ce moment-là.

Règle de la chaîne

Une fonction f (x, y) Avec des dérivés partiels continus en X et et, qui à son tour dépend d'un paramètre t à travers de x = x (t) et y = y (t), Il a une dérivée ordinaire par rapport à la variable t, qui est calculé par la règle de la chaîne:

d_t Z = ∂_Xz D_tx + ∂_etz D_tet

Propriété de fermeture ou de verrouillage

La dérivée partielle par rapport à l'une des variables d'une fonction F de deux variables ou plus (X, y, ...), C'est une autre fonction g Dans ces mêmes variables, par exemple: 

G (x, y, ...) = ∂_et f (x, y, ...)

C'est-à-dire que la dérivation partielle est une opération qui va de rⁿ A Rⁿ. En ce sens, il est dit que c'est un opération fermée.

Dérivés partiels successifs

Les dérivés partiels successifs d'une fonction de plusieurs variables peuvent être définis, donnant naissance à de nouvelles fonctions dans les mêmes variables indépendantes.

Être la fonction f (x, y). Les dérivés successifs suivants peuvent être définis:

F_Xx = ∂_XF ;  F_Oui = ∂_OuiF ; F_Xy = ∂_XyF et F_Yx = ∂_YxF

Les deux derniers sont connus comme Dérivés mixtes Parce qu'ils impliquent deux variables indépendantes différentes.

Théorème de Schwarz

Être une fonction f (x, y), défini de telle manière que ses dérivés partiels sont des fonctions continues dans un sous-ensemble ouvert de R².

Donc, pour chaque paire (X, y) Qu'ils appartiennent à ce sous-ensemble, les dérivés mixtes sont identiques:

∂_XyF = ∂_YxF

La déclaration précédente est connue sous le nom Théorème de Schwarz.

Comment les dérivés partiels sont-ils calculés?

Les dérivés partiels sont calculés similaires aux dérivés de fonctions ordinaires dans une seule variable indépendante. Lorsque la dérivée partielle d'une fonction de plusieurs variables est prise par rapport à l'une d'elles, les autres variables sont prises sous forme de constantes.

Peut vous servir: moitié de 15

Vous trouverez ci-dessous plusieurs exemples:

Exemple 1

Être la fonction:

f (x, y) = -3x² + 2 (et - 3)²

Il est invité à calculer le premier dérivé partiel en ce qui concerne X et le premier dérivé partiel par rapport à et.

Procédure

Pour calculer le partiel F à l'égard de X, se prend et Comme constant:

∂_XF = ∂_X(-3x² + 2 (et - 3)² ) = ∂_X(-3x² ) + ∂_X(2 (et - 3)² ) = -3 ∂_X(X²) + 0 = -6x.

Et à son tour, pour calculer le dérivé par rapport à et se prend X Comme constant:

∂_etF = ∂_et(-3x² + 2 (et - 3)² ) = ∂_et(-3x² ) + ∂_et(2 (et - 3)² ) = 0 + 2 · 2 (y - 3) = 4y - 12.

Exemple 2

Déterminer les dérivés partiels de second ordre:  ∂_Xxf, ∂_Ouif, ∂_YxF et ∂_XyF Pour la même fonction F de l'exemple 1.

Procédure

Dans ce cas, car la première dérivée partielle est déjà calculée en X et et (Voir l'exemple 1):

∂_XxF = ∂_X(∂_Xf) = ∂_X(-6x) = -6

∂_OuiF = ∂_et(∂_etf) = ∂_et(4y - 12) = 4

∂_YxF = ∂_et(∂_Xf) = ∂_et(-6x) = 0

∂_XyF = ∂_X(∂_etf) = ∂_X(4y - 12) = 0

Il est observé que ∂_YxF = ∂_XyF, réalisant ainsi le théorème de Schwarz, depuis la fonction F et ses dérivés partiels de premier ordre sont toutes des fonctions continues R².

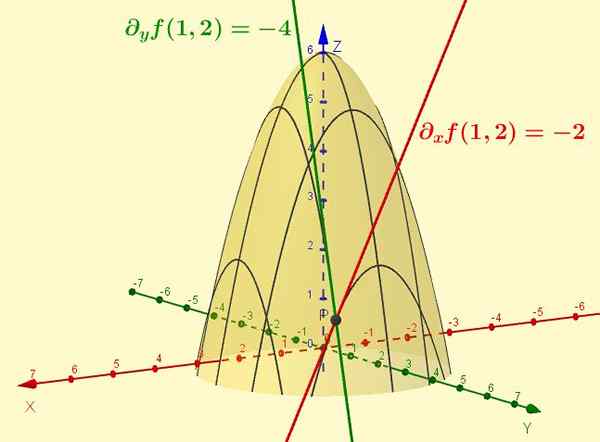
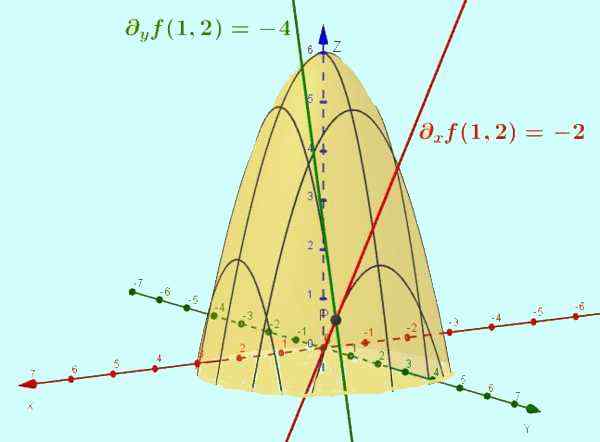Figure 2. La fonction z = f (x, y) = -x2 - y2 + 6 est la surface illustrée sur la figure. La dérivée partielle par rapport à X est la pente de la ligne tangente de la courbe qui résulte de l'intersection de ladite surface avec le plan y = CTTE (le cas particulier est montré y = 2). De même, la partie de F par rapport à et est la pente de la tangente à l'intersection avec x = 1, au point (1, 2, 1).

Exercices résolus

Exercice 1

Être la fonction:

Peut vous servir: successions quadratiques: exemples, règles et exercices résolus

f (x, y) = -x² - et² + 6

Trouver des fonctions G (x, y) = ∂_XF  et H (x, y) = ∂_etF.

Solution

Le dérivé partiel de F à l'égard de X, pour lequel la variable et Il devient constant:

G (x, y) = - 2x

De même, la dérivée partielle de g à l'égard de et, action X constant, résultant de la fonction H:

H (x, y) = -2y

Exercice 2 

Évaluer le point (1, 2) les fonctions f (x, y) et G (x, y) de l'exercice 1. Interpréter les résultats.

Solution

Les valeurs sont remplacées x = 1 et y = 2 obtention:

f (1,2) = - (1)² -(2)² + 6 = -5 + 6 = 1

C'est la valeur qui prend la fonction F lorsqu'il est évalué à ce point.

La fonction f (x, y) C'est une surface à deux dimensions et coordonnée z = f (x, y) C'est la hauteur de la fonction pour chaque paire (X, y). Quand la paire est prise (1.2), La hauteur de surface f (x, y) est Z = 1.

La fonction G (x, y) = - 2x représente un plan dans l'espace à trois dimensions dont l'équation est Z = -2x ou bien -2x + 0 et -z = 0.

Ledit avion est perpendiculaire à l'avion Xz Et passez par le point (0, 0, 0). Lorsqu'il est évalué dans x = 1 et y = 2 ensuite Z = -2. Notez que la valeur z = g (x, y) Il est indépendant de la valeur attribuée à la variable et.

D'un autre côté, si la surface se croise f (x, y) Avec l'avion y = c, avec c constant, vous avez une courbe dans le plan Zx: z = -x² - c² + 6.

Dans ce cas le dérivé de z à l'égard de X coïncide avec le dérivé partiel de f (x, y) à l'égard de X: d_X Z = ∂_XF .

Lors de l'évaluation dans la paire (x = 1, y = 2) Le dérivé partiel à ce moment ∂_XF (1.2) Il est interprété comme la pente de la ligne tangente à la courbe z = -x² + 2 Sur le point (x = 1, y = 2) Et la valeur de cette pente est -2.

Les références

1. Ayres, f. 2000. Calcul. 5ed. Mc Graw Hill.
2. Dérivés partiels d'une fonction dans plusieurs variables. Récupéré de: construire.UPM.est.
3. Leithold, L. 1992. Calcul avec géométrie analytique. Harla, s.POUR.
4. Purcell, E. J., Varberg, D., & Rigdon, s. ET. (2007). Calcul. Mexique: Pearson Education.
5. Gorostizaga J. C. Dérivés partiels. Récupéré de: ehu.EUS
6. Wikipédia. Dérivée partielle. Récupéré de: est.Wikipédia.com.