Dérivés algébriques

Quels sont les dérivés algébriques?

Le dérivés algébriques Ils sont constitués de l'étude du dérivé dans le cas particulier des fonctions algébriques. L'origine de la notion de dérivé remonte à la Grèce antique. Le développement de cette notion a été motivé par la nécessité de résoudre deux problèmes importants, un en physique et un en mathématiques.

En physique, le dérivé résout le problème de la détermination de la vitesse instantanée d'un objet en mouvement. En mathématiques, il permet de trouver la ligne tangente à une courbe à un moment donné.

Bien qu'il y ait vraiment beaucoup plus de problèmes qui sont résolus en utilisant le dérivé, ainsi que ses généralisations, les résultats qui sont venus plus tard à l'introduction de leur concept.

Les pionniers du calcul différentiel sont Newton et Leibniz. Avant de donner la définition formelle, nous développerons l'idée derrière, du point de vue mathématique et physique.

Le dérivé en attente de la ligne tangente à une courbe

Supposons que le graphique d'une fonction y = f (x) soit un graphique continu (sans pointes ou sommets ou séparations), et soit a = (a, f (a)) un point fixe sur. Nous voulons trouver l'équation de ligne tangente à la fonction F au point A.

Prenons un autre point P = (x, f (x)) du graphique, près du point A, et tracez la ligne de séchage qui passe par A et P. Une ligne de séchage est une ligne qui coupe le graphique d'une courbe en un ou plusieurs points.

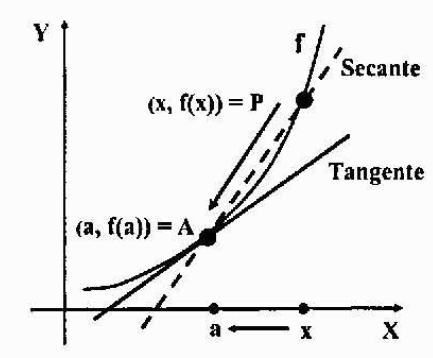
Pour obtenir la ligne tangente que nous voulons, il est seulement nécessaire de calculer la pente car nous avons déjà un point de ligne: le point A.

Si nous déplaçons le point P par le graphique et que nous l'approdissons de plus en plus au point A, la ligne sèche mentionnée précédemment s'approchera de la ligne tangente que vous souhaitez trouver. Prenant la limite lorsque "p tend à un", les deux lignes coïncidront, donc leurs pentes.

La pente de la ligne sécante est donnée par

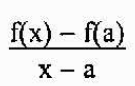
Dire que P est proche de A, équivaut à dire que "x" approche "A". Ainsi, la pente de la ligne tangente au graphique de f au point A sera égale à:

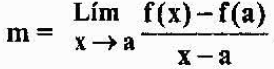
L'expression précédente est indiquée par f '(a), et est définie comme la dérivée d'une fonction f au point "a". Nous voyons qu'analytiquement, la dérivée d'une fonction à un point est une limite, mais géométriquement, c'est la pente de la ligne tangente au graphique de la fonction au point.

Peut vous servir: variable aléatoire: concept, types, exemples

Maintenant, nous verrons cette notion du point de vue de la physique. Nous atteindrons la même expression de la limite précédente, bien que par un chemin différent, obtenant ainsi unanimité de la définition.

Le dérivé comme vitesse instantanée d'un objet en mouvement

Regardons un bref exemple de ce que signifie la vitesse instantanée. Quand il est dit, par exemple, qu'une voiture pour atteindre une destination l'a fait à une vitesse de 100 km par heure, ce que cela signifie, c'est qu'en une heure, il a parcouru 100 km.

Cela ne signifie pas nécessairement que pendant toute l'heure, la voiture était toujours de 100 km, le vecimeter de la voiture pourrait à certains moments moins ou plus. S'il avait besoin de se tenir à un feu de circulation, la vitesse à ce moment était de 0 km. Cependant, après une heure, l'itinéraire était de 100 km.

C'est ce que l'on appelle la vitesse moyenne et est donné par le quotient de la distance parcourue entre le temps écoulé, comme nous venons de le voir. La vitesse instantanée, quant à elle, est celle qui marque l'aiguille de vélocimètre d'une voiture à un certain instant (temps).

Voyons cela maintenant plus général. Supposons qu'un objet se déplace le long d'une ligne et que ce déplacement est représenté au moyen de l'équation s = f (t), où la variable T mesure le temps et la variable S le déplacement, en tenant compte de son début dans le moment t = 0, à quel moment il est également nul, c'est-à-dire f (0) = 0.

Cette fonction f (t) est connue sous le nom de fonction de position.

Une expression pour la vitesse instantanée de l'objet est recherchée à un instant fixe. À cette vitesse, nous le désignerons par V (A).

Que ce soit à tout moment proche de "A" instantanément. Dans l'intervalle de temps entre «A» et «T», le changement de position est donné par F (t) -f (A).

La vitesse moyenne dans cet intervalle de temps est:

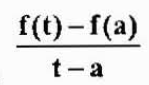
Qui est une approximation de la vitesse instantanée V (a). Cette approche sera meilleure car T se rapproche de "A". Donc,

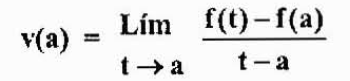
Notez que cette expression est égale à celle obtenue dans le cas précédent, mais dans une perspective différente. C'est ce que l'on appelle la dérivée d'une fonction F à un point "a" et est désignée par f '(a), comme indiqué ci-dessus.

Peut vous servir: lois des exposants

Notez que faire le changement h

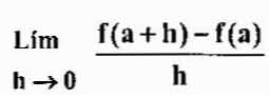
Les deux expressions sont équivalentes mais parfois elles doivent être utilisées plus à l'une au lieu de l'autre, selon l'affaire.

Il est ensuite défini plus généralement celui dérivé d'une fonction f à tout moment "x" appartenant à son domaine comme

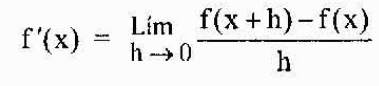
La notation la plus habituelle pour représenter la dérivée d'une fonction y = f (x) est celle que nous venons de voir (f 'o y'). Cependant, une autre notation largement utilisée est la notation de Leibniz qui est représentée comme l'une des expressions suivantes:

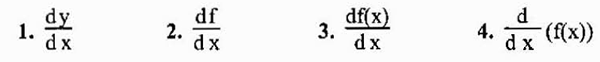
Compte tenu du fait que le dérivé est essentiellement une limite, il peut exister ou non, car les limites n'existent pas toujours. Dans le cas où il existe, il est dit que la fonction en question est différenciable au point donné.

Fonction algébrique

Une fonction algébrique est une combinaison de polynômes à travers des sommes, des soustractions, des produits, des quotients, des pouvoirs et des radicaux.

Un polynôme est une expression de forme

P_n= A_nXⁿ+ pour_N-1X^N-1+ pour_N-2X^N-2+… + A₂X²+ pour₁x + a₀

Où n est un nombre naturel et tous les_Toi, Avec i = 0,1,…, n sont des nombres rationnels et_n≠ 0. Dans ce cas, on dit que le degré de ce polynôme est n.

Voici des exemples de fonctions algébriques:

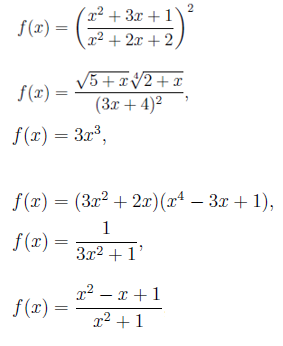
Ici, les fonctions exponentielles, logarithmiques et trigonométriques ne sont pas incluses. Les règles de dérivation que nous verrons ci-dessous sont valables pour les fonctions en général, mais nous les limiterons et les appliquerons dans le cas des fonctions algébriques.

Règles de derrying

Dérivé d'une constante

Déclare que le dérivé d'une constante est nul. C'est-à-dire si f (x) = c, alors f '(x) = 0. Par exemple, la dérivée de la fonction constante 2 est égale à 0.

Dérivé d'un pouvoir

Si f (x) = xⁿ, alors f '(x) = nx^N-1. Par exemple, x dérivé³ C'est 3x². En conséquence, il est obtenu que le dérivé de la fonction d'identité f (x) = x est f '(x) = 1x^1-1= x⁰= 1.

Un autre exemple est le suivant: Soit f (x) = 1 / x², alors f (x) = x^-2 et f '(x) = -2x^-2-1= -2x^-3.

Cette propriété est également des racines valables, car les racines sont des pouvoirs rationnels et ce qui précède peut également être appliqué dans ce cas. Par exemple, la dérivée d'une racine carrée est donnée par

Il peut vous servir: estimation par intervalles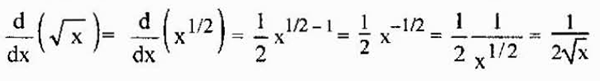

Dérivé d'une somme et d'une soustraction

Si f et g sont des fonctions différenciables dans x, alors la somme f + g est également et il est rempli que (f + g) '(x) = f' (x) + g '(x) (x) (x).

De même, vous devez (f-g) '(x) = f' (x) -g '(x). En d'autres termes, le dérivé d'une somme (soustraction) est la somme (ou la soustraction) des dérivés.

Exemple

Si h (x) = x²+X-1, alors

H '(x) = (x²) + (x) '- (1)' = 2x + 1-0 = 2x + 1.

Produit dérivé d'un produit

Si F et G sont des fonctions différenciables dans X, alors le produit FG est également différenciable dans X et il est rempli que

(fg) '(x) = f' (x) g (x) + f (x) g '(x).

En conséquence, il a si C est une constante et que f est une fonction différenciable dans x, alors CF est également différenciable dans x y (cf) '(x) = cf' (x).

Exemple

Si f (x) = 3x (x²+1), alors

f '(x) = (3x)' (x²+1) + (3x) (x²+1) '= 3 (x)' (x²+1) + 3x [(x²) '+ (1)]

= 3 (1) (x²+1) + 3x [(2x^2-1) +0] = 3 (x²+1) + 3x (2x) = 3x²+3 + 6x²

= 9x²+3.

Dérivé d'un quotient

Si f et g sont différenciables en x et g (x) ≠ 0, alors f / g est également différenciable dans x, et il est accompli que

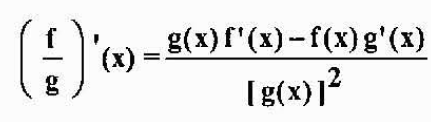
Exemple: Si h (x) = x³/(X²-5x), alors

H '(x) = [(x³) '(X⁵-5x) - (x³) (X⁵-5x) '] / (x⁵-5x)²= [(3x²) (X⁵-5x) - (x³) (5x⁴-5)] / (x⁵-5x)².

Règle de la chaîne

Cette règle permet de dériver la composition des fonctions. Il établit ce qui suit: Si y = f (u) est différenciable en u et u = g (x) est différenciable dans x, alors la fonction composée f (g (x)) est différenciable dans x, et il est rempli que [f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f g (x))]] '= f' (g (x)) g '(x).

C'est-à-dire que la dérivée d'une fonction composée est le produit de la dérivée de la fonction externe (dérivé externe) par la fonction interne dérivée (dérivé interne).

Exemple

Si f (x) = (x⁴-2x)³, ensuite

f '(x) = 3 (x⁴-2x)²(X⁴-2x) '= 3 (x⁴-2x)²(4x³-2).

Il y a également des résultats pour calculer la dérivée inverse d'une fonction, ainsi que la généralisation aux dérivés d'ordre supérieur. Les applications sont étendues. Parmi eux, leurs bénéfices dans l'optimisation et les fonctions minimales sont mis en évidence.

Les références

1. Alarcon, s., González, m., & Quintana, H. (2008). Calcul différentiel. Itm.
2. Cabrera, V. M. (1997). 4000 calculs. Progreso éditorial.
3. Castaño, h. F. (2005). Mathématiques avant le calcul. Université de Medellin.
4. Eduardo, n. POUR. (2003). Introduction au calcul. Éditions ombral.
5. Sources, un. (2016). Mathématiques de base. Une introduction au calcul. Lulu.com.
6. Purcell, E. J., Rigdon, s. ET., & Varberg, D. ET. (2007). Calcul. Pearson Education.
7. Saenz, J. (2005). Calcul différentiel (Deuxième Ed.). Barquisimeto: Hypotenusa.
8. Thomas, G. B., & Weir, m. D. (2006). Calcul: plusieurs variables. Pearson Education.