Quels sont les diviseurs de 30? (Explication)
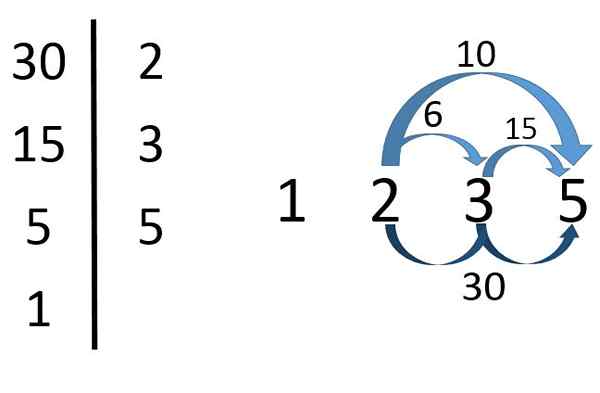
- 5035
- 299
- Paul Dumas
Les diviseurs de 30 sont 1, 2, 3, 5, 6, 10, 15 et 30. Nous expliquons pourquoi et comment vous pouvez le calculer par vous-même.
Rapidement, peut être connu Quels sont les diviseurs de 30, ainsi que tout autre nombre (différent de zéro), mais l'idée fondamentale est d'apprendre comment les diviseurs d'un nombre sont calculés de manière générale.
Il faut prendre soin de parler de diviseurs, car il peut être rapidement établi que tous les diviseurs de 30 sont 1, 2, 5, 6, 10, 15 et 30, mais qu'en est-il des négatifs de ces chiffres? Sont des diviseurs ou non?
Pour répondre à la question précédente, il est nécessaire de comprendre un terme très important dans le monde des mathématiques: l'algorithme de division.
Algorithme de division
L'algorithme de division (ou division euclidienne) indique ce qui suit: Compte tenu de deux entiers "n" et "b", étant "b" différent de zéro (b ≠ 0), il y a un "q" et un "r" uniques, tels que n = bq + r, où 0 ≤ r < |b|.
Le numéro "n" est appelé dividende, "b" est appelé diviseur, "Q" est appelé quotient et "r" est appelé le reste ou les déchets. Lorsque le reste "r" est égal à 0, il est dit que "B" divise "n", et cela est désigné par "b | n".
L'algorithme de division ne se limite pas aux valeurs positives. Par conséquent, un nombre négatif peut être diviseur d'un autre nombre.
Pourquoi 7.5 n'est pas un diviseur de 30?
En utilisant l'algorithme de division, on peut voir que 30 = 7,5 × 4 + 0. Le reste est égal à zéro, mais on ne peut pas dire que 7,5 divise 30 parce que, lorsque vous parlez de diviseurs, seuls des nombres entiers sont en train de parler.
Peut vous servir: fonction exponentielle: propriétés, exemples, exercicesDiviseurs de 30
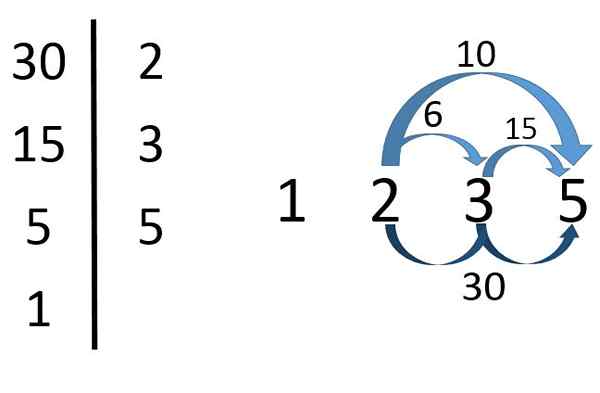 Diviseurs de 30
Diviseurs de 30 Comme on peut le voir dans l'image, pour trouver les diviseurs de 30 premiers, leurs facteurs premiers doivent être trouvés.
Alors, 30 = 2x3x5. De là, il est conclu que 2, 3 et 5 Ce sont des diviseurs de 30. Mais les produits de ces facteurs premiers aussi.
De sorte que 2 × 3 =6, 2 × 5 =dix, 3 × 5 =quinze et 2x3x5 =30 Ce sont des diviseurs de 30. Il 1 C'est aussi un diviseur de 30 (bien qu'en réalité c'est un diviseur de n'importe quel nombre).
On peut conclure que 1, 2, 3, 5, 6, 10, 15 et 30 sont des diviseurs de 30 (Tout le monde remplit l'algorithme de division), mais nous devons nous rappeler que leurs négatifs sont également des diviseurs.
Par conséquent, tous les diviseurs de 30 sont: -30, -15, -10, -6, -5, -3, -2, -1, 1, 2, 3, 5, 6, 10, 15 et 30.
Ce qui a été appris ci-dessus peut être appliqué avec n'importe quel numéro entier.
Par exemple, si vous souhaitez calculer les diviseurs de 92, procédez comme avant. Il se décompose en tant que produit de nombres premiers.
92 est divisé par 2 et obtenu 46; Maintenant, 46 est à nouveau divisé par 2 et obtient 23.
Ce dernier résultat est un nombre premier, il n'aura donc pas plus de diviseurs en plus de 1 et du même 23.
Nous pouvons alors écrire 92 = 2x2x23. En procédant comme auparavant, il est conclu que les 1,2,46 et 92 sont 92 diviseurs.
Enfin, les négatifs de ces chiffres à la liste précédente sont inclus, qui est la liste de tous les diviseurs de 92 est -92, -46, -4, -2, -1, 1, 2, 4, 46, 46, 92.
- « Activités pour les enfants ayant des problèmes d'apprentissage
- Combien de centièmes s'adaptent dans un dixième? (Exemples) »

