Formule et équations de la quasi-élément, exemples, exercice

La évaluation quasi, La variance quasi ou la variance malsaine est une mesure statistique de la dispersion des données d'un goûter Concernant la moyenne. L'échantillon consiste à son tour en une série de données prises à partir d'un univers majeur, appelé Ville.

Il est indiqué de plusieurs manières, ici il a été choisi s_c² Et pour le calculer, la formule suivante suit:

Figure 1. La définition de la quasivité. Source: F. Zapata.

Où:

-s_c ² = la quasiriance ou la variance de l'échantillon (variance de l'échantillon)

-X_Toi = Chacune des données d'échantillons

-n = nombre d'observations

-X = La moyenne de l'échantillon

Étant donné que l'unité de l'échantillon Quasivesive est le carré de l'unité dans laquelle l'échantillon arrive, au moment de l'interprétation des résultats, il est préféré de travailler avec le quasi écart type ou écart-type de l'échantillon.

Ceci est désigné comme s_c Et il est obtenu en extrait la racine carrée de la quasivariance:

s_c = √ s_c ²

La quasiriance est similaire à la variance s², avec la seule différence que dans le dénominateur de cela est N-1, tandis que dans la variance, il n'est divisé que par n. Il est évident que lorsque N est très grand, les valeurs des deux ont tendance à être les mêmes.

Lorsque la valeur de la quasiriance est connue, vous pouvez immédiatement savoir celle de la variance.

[TOC]

Exemples de bizarre

Vous voulez connaître les caractéristiques de toute population: les personnes, les animaux, les plantes et en général tout type d'objets. Mais l'analyse de l'ensemble de la population peut ne pas être une tâche facile, surtout si le nombre d'éléments est très important.

Ensuite, des échantillons sont prélevés, dans l'espoir que leur comportement reflète celui de la population et puisse donc en faire des inférences, grâce à quelles ressources sont optimisées. Ceci est connu comme inférence statistique.

Voici quelques exemples dans lesquels la quasiriance et l'écart type associé à quasi servent d'indicateur statistique en soulignant que les résultats obtenus en ce qui concerne la moyenne.

Il peut vous servir: périmètre du cercle: comment le retirer et formules, exercices résolus

1.- Le directeur marketing d'une entreprise qui fabrique des batteries de voitures doit estimer, en mois, la durée moyenne des batteries.

Pour ce faire, sélectionnez au hasard un échantillon de 100 batteries de cette marque achetée. L'entreprise conserve un enregistrement des données des acheteurs et peut les interviewer pour connaître la durée des batteries.

Figure 2. L'évaluation cuasive est utile pour faire des inférences et un contrôle de la qualité. Source: Pixabay.

2.- La gestion académique d'une institution universitaire doit estimer l'enregistrement de l'année suivante, analysant le nombre d'étudiants qui devraient approuver les matières actuellement.

Par exemple, de chacune des sections qui étudient actuellement le sujet physique I, l'adresse peut sélectionner un échantillon d'étudiants et analyser ses performances dans ladite chaise. De cette façon, vous pouvez déduire combien d'étudiants étudieront la physique II dans la prochaine période.

3.- Un groupe d'astronomes concentre leur attention sur une partie du ciel, où un certain nombre d'étoiles avec certaines caractéristiques sont observées: taille, masse et température par exemple.

Il vaut la peine de demander si les étoiles dans une autre région similaire auront ces mêmes caractéristiques, y compris les étoiles d'autres galaxies, comme les nuages ​​voisins de Magallanes ou Andromeda.

Pourquoi diviser entre N-1?

Dans la quasiriance, il est divisé entre N-1 au lieu de n Et c'est parce que la quasiriance est un Estimateur insisté, Comme indiqué au début.

Il arrive que parmi la même population, il est possible d'extraire de nombreux échantillons. La variance de chacun de ces échantillons peut également être moyenne, mais la moyenne de ces variances ne s'avère pas être égale à la variance de la population.

Peut vous servir: valeur relative

En fait, la moyenne des variances de l'échantillon a tendance à sous-estimer la variance de la population, sauf si elle est utilisée N-1 Dans le dénominateur. Il peut être vérifié que le valeur attendue de la quasivité e (s_c²) est précisément s².

C'est pourquoi il est dit que la quasiriance est inscrite et est un meilleur estimateur de la variance de la population S².

Moyen alternatif de calculer l'évaluation quasive

Il est facilement démontré que la quasiriance peut également être calculée comme suit:

s_c² = [∑x² / (N -1)] - [∑nx² / (N-1)]

Le score standard

En ayant l'écart par rapport à l'échantillon, nous pouvons savoir combien d'écarts-types ont une valeur particulière x, au-dessus ou en dessous de la moyenne.

Pour cela, l'expression sans dimension suivante est utilisée:

Score standard = (x - x) / s_c

Exercice résolu

Calculez la quasiriance et la déviation quasi-typique des données suivantes, qui se composent de paiements mensuels en $ effectué par une compagnie d'assurance à une clinique privée.

863 903 957 1041 1138 1204 1354 1624 1698 1745 1802 1883

a) Utilisez la définition de la quasivité donnée au début et vérifiez également le résultat par la forme alternative donnée dans la section précédente.

b) Calculez le score standard des deuxième données, lisant de haut en bas.

Solution à

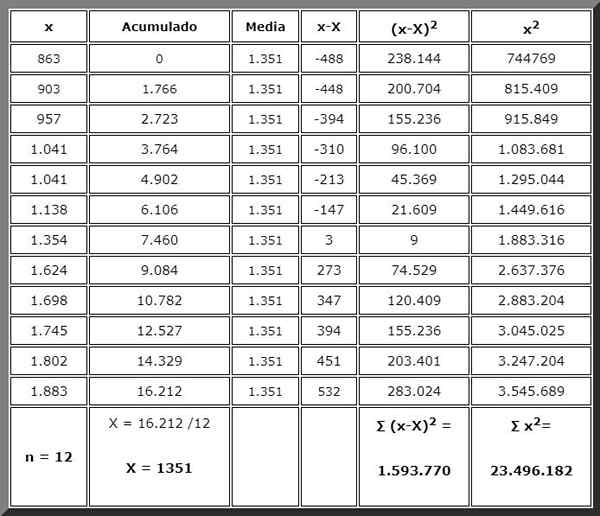
Le problème peut être résolu à la main à l'aide d'une calculatrice simple ou scientifique, pour laquelle nous devons procéder dans l'ordre. Et pour cela rien de mieux que d'organiser les données dans un tableau comme celui ci-dessous:

Grâce au tableau, vous avez organisé des informations et les montants qui seront nécessaires dans les formules sont à la fin des colonnes respectives, prêtes à l'emploi immédiatement. Les résumés sont indiqués en gras.

Peut vous servir: quels sont les 7 éléments de la circonférence?

La colonne moyenne est toujours répétée, mais cela en vaut la peine car il est pratique d'avoir la valeur en vue, de remplir chaque rangée du tableau.

Enfin, l'équation de la quasiriance donnée au début est appliquée, seules les valeurs sont remplacées et en termes de somme, nous l'avons déjà calculé:

s_c² = 1.593.770 / (12-1) = 1.593.770/11 = 144.888.2

C'est la valeur de la quasiriance et ses unités sont des «dollars au carré», ce qui n'a pas beaucoup de sens, de sorte que les quasides standard de l'échantillon sont calculés, qui n'est rien de plus que la racine carrée de la quasivariance:

s_c = (√144.888.2) $ = 380,64 $

Il est immédiatement corroboré que cette valeur est également obtenue avec la forme alternative de la quasivariance. La somme nécessaire est à la fin de la dernière colonne à gauche:

s_c² = [∑x² / (N-) - [∑nx² / (N-1)] = [23.496.182/11] - [12 x 1351²/ onze]

= 2.136.016.55 - 1.991.128,36 = 144.888 $ au carré

C'est la même valeur obtenue avec la formule donnée au début.

Solution B

La deuxième valeur de haut en bas est de 903, son score standard est

Score standard de 903 = (x - x) / s_c = (903 - 1351) / 380.64 = -1.177

Les références

1. Canavos, g. 1988. Probabilité et statistiques: applications et méthodes. McGraw Hill.
2. Devore, J. 2012. Probabilité et statistiques pour l'ingénierie et la science. 8e. Édition. Cengage.
3. Levin, R. 1988. Statistiques pour les administrateurs. 2e. Édition. Prentice Hall.
4. Mesures de dispersion. Récupéré de: Thales.Cica.est.
5. Walpole, R. 2007. Probabilité et statistiques pour l'ingénierie et la science. Pearson.