Conclusion de vitesse

Quelle est la constante de vitesse?

La Conclusion de vitesse C'est une constante de proportionnalité de la loi de vitesse de la cinétique chimique, qui établit une relation entre la concentration molaire des réactifs et la vitesse de la réaction.

À mesure que les réactifs, les vitesses de réaction consomment également,. C'est pourquoi dans les calculs de la constante de vitesse, représentés par le symbole «K», les vitesses initiales sont prises en compte, pour avoir un point de comparaison entre plusieurs expériences.

La cinétique chimique indique que cette constante dépend des ordres de réaction des réactifs, dont les concentrations modifieront la vitesse de la réaction.  D'un autre côté, selon l'équation d'Arrhenius, k dépend également de la température et de l'énergie d'activation pour la réaction.

C'est pourquoi il est dit que la constante de vitesse n'est pas une véritable constante, car elle varie avec la température et aussi avec la présence de catalyseurs qui modifient l'énergie d'activation. Par conséquent, il n'y a pas beaucoup de tables où ils viennent pour des réactions (et des conditions) spécifiques.

Par exemple, pour une réaction où A et B réagissent, chacun avec un ordre de réaction de 1, la constante rapportée K à 25 ° C, et avec l'ajout d'une certaine quantité de catalyseur, ce ne sera pas la même si la réaction est fait à une température de 26 ou 27 ºC. La moindre variation affectera la valeur de k, qui n'est constante que pendant les conditions établies pour les expériences.

Comment calculer la constante de vitesse?

Expérimentation

La détermination de la valeur de la constante de vitesse d'une réaction est faite expérimentalement. Si, par exemple, vous souhaitez déterminer la valeur de la constante de vitesse pour une réaction de la forme:

A + B → C

Pour l'établissement de la valeur de K, trois réactions peuvent être effectuées, avec les différences suivantes: dans la réaction 2 La concentration initiale de réactif A est constante, [A], mais est doublé, par exemple, la concentration de réactif B, [ B].

Entre-temps, dans la réaction 3 [a] est doublé par rapport à la réaction 1, en gardant constant [B].

Ainsi, un tableau de concentrations sera construit qui servira à comparer les vitesses initiales entre plusieurs expériences. Ceci dans le but de déterminer les ordres de réaction, et consécutivement pour calculer la vitesse constante.

Peut vous servir: hydroxyde d'aluminium: structure, propriétés, utilisations, risques

Ordres de réaction

Premier calcul

Pour la réaction précédente, sa vitesse est exprimée par l'équation:

Vitesse de réaction = k · [a]^X· [B]^et

Où 'x' e 'et' correspondent aux ordres de réaction pour les réactifs A et B, respectivement.

Pour déterminer les valeurs des ordres de réaction, une comparaison entre la réaction 2 et 1, ainsi qu'entre la réaction 3 et 1 doivent être faites.

Lors de la comparaison de la réaction 1 avec le 2, il pourrait être observé, par exemple, qu'en duplication [b], il y a une duplication de la vitesse de réaction.

Alors: la proportion de [b] entre les réactions 2 et 1 est 2, ainsi que la proportion entre les vitesses des réactions. Ensuite, la valeur de l'ordre de la réaction peut être obtenue par rapport à B (exposant et), par l'approche suivante:

Calcul de l'ordre de réaction 'et'. Source: Gabriel Bolívar.

La vitesse de l'expérience 2 est deux fois plus rapide que la vitesse de l'expérience 1. Ainsi, en divisant les deux équations ci-dessus, nous aurons:

2 = 2^et

Par conséquent, «et« Vale 1, être capable de conclure que l'ordre de la réaction par rapport au réactif B est du premier ordre.

Deuxième calcul

De la même manière, nous procédons avec le réactif A pour le calcul de «x»:

Calcul de l'ordre de réaction 'x'. Source: Gabriel Bolívar.

La vitesse de l'expérience ou de la réaction 3 est quatre fois plus élevée que l'expérience ou la réaction 1. Donc:

4 = 2^X

SOIT

2² = 2^X

Et la valeur de x est 2, donc la réaction est de deuxième ordre par rapport au réactif à.

Claitement final

Ensuite, la valeur de la constante de vitesse basée sur l'une des réactions peut être établie:

Vitesse de réaction = k · [a]²· [B]

Assez pour introduire des valeurs expérimentales et effacer K:

K = vitesse de réaction / ([a]²· [B])

Exemples

Les exemples suivants servent d'introduction avant les exercices résolus dans la section suivante.

Exemple 1

Dans une réaction chimique:

a) Si la concentration initiale d'un réactif est doublé la vitesse de la réaction: quel est l'ordre de la réaction par rapport à ce réactif?

b) Si l'augmentation de la concentration de réactifs provoque une augmentation de la vitesse d'un facteur de 8, quel serait alors l'ordre de réaction?

c) Si la concentration du réactif subit un changement et que la vitesse reste la même: quel est l'ordre de la réaction par rapport au réactif?

Il peut vous servir: Cycopropane (C3H6)

Dans a) la proportion de vitesses de réaction est la même et la proportion de concentrations de réactifs est égale à 2^X,

2 = 2^X

Par conséquent, x = 1 et l'ordre de la réaction par rapport au réactif est 1.

En b) la proportion de la vitesse de réaction est la même 8 (2³) et la proportion de concentrations de réactifs est égale à 2^X,

2³ = 2^X

Par conséquent, x = 3 et l'ordre de la réaction par rapport au réactif est 3-

Tandis que c) la vitesse de la réaction est indépendante de la concentration du réactif, de sorte que l'ordre de la réaction par rapport au réactif est nul.

Exemple 2

La réaction:

2 Non₂  +  SOIT₂ → 2 Non₂

Il a l'expression de la loi de vitesse suivante:

Vitesse de réaction = k · [non₂]]²·SOIT₂.

Quel est l'ordre mondial de la réaction? Quelles unités k auraient?

L'ordre de la réaction concernant ou₂ C'est 1, et l'ordre de la réaction par rapport à non₂ C'est 2, donc l'ordre global de la réaction est la somme de ces valeurs, c'est-à-dire 2 + 1 = 3.

La vitesse de la réaction a des unités M / S, et les concentrations des réactifs sont exprimées en m. Faire une analyse des unités que nous aurons:

k = vitesse de réaction / ([non₂]]²·[SOIT₂]]

= (M / s) / (m³)

= s^-1M^-2

Exercices résolus

Exercice 1

Les données de la réaction suivante ont été obtenues à 25 ° C:

A +2 B → C +2 D

Quelle est l'expression de la loi de vitesse de cette réaction? Quelle est la valeur de votre constante de vitesse?

Calculs des ordres de réaction

Les données expérimentales sont:

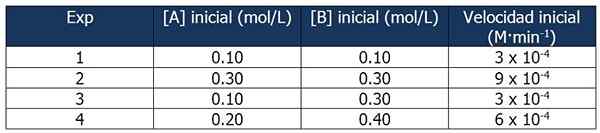Données cinétiques de l'exercice 1. Source: Gabriel Bolívar.

La comparaison des expériences 1 et 3 vous permet de tirer les conclusions suivantes:

Proportion entre les vitesses des réactions 3 et 1:

3 x 10^-4 M · Min^-1 / 3 x 10^-4 M · Min^-1 = 1

Mais la proportion entre les concentrations de B est:

(0.3 mol / l) / (0.1 mol / l) = 3

La vitesse de la réaction est indépendante de la concentration de B, car son augmentation ne l'affecte pas. Par conséquent, l'ordre de la réaction par rapport au réactif B est nul.

D'un autre côté, la comparaison des réactions 4 et 1 permet les conclusions suivantes:

6 x 10^-4 M · Min^-1 / 3 x 10^-4 M · Min^-1 = 2

Entre-temps, la proportion entre [a] des réactions 4 et 1 est égale à:

Peut vous servir: 5 caractéristiques des mélanges homogènes

(0.20 mol / l) / (0.10 mol / l) = 2^X

Ensuite, la relation entre les proportions sera:

2 = 2^X

x = 1

Par conséquent, l'expression de la loi sur la vitesse est:

Vitesse de réaction = k · [a]

B n'est pas pris en charge parce que son ordre de réaction est nul.

Calcul de K

Nous pouvons calculer la vitesse constante à partir de l'une des données cinétiques. Utilisons l'expérience 1:

K = vitesse de réaction / [a]

= 3 x 10^-4 M · Min^-1 / 0.10 m

= 3 x 10^-3 ou 0.003 min^-1

Exercice 2

Les données de vitesse de réaction ont été obtenues à une certaine température.

2 CLO₂ (AC) +2 Oh^- (AC) → CLO₃^- (AC) + CLO₂ (AC) + H₂Ou (l)

Calculs des ordres de réaction

Les données expérimentales sont:

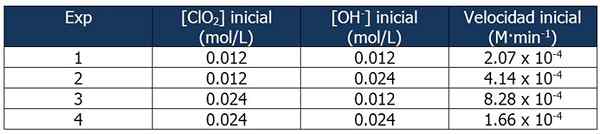Données cinétiques sur l'exercice 2. Source: Gabriel Bolívar.

La proportion entre les vitesses de réaction 2 et la réaction 1 est:

4.14 x 10^-4 M · Min^-1 / 2.07 x 10^-4 M · Min^-1 = 2

Et la proportion de concentrations OH^- Entre les réactions 2 et 1 est égale à:

(0,024 mol / L) / (0,012 mol / L) = 2^X

L'exposant «x» représente l'ordre de la réaction par rapport au réactif OH^-. La relation entre les proportions calculées peut être représentée comme suit:

2 = 2^X

x = 1

Par conséquent, l'ordre de la réaction par rapport au réactif OH^- est égal à 1.

En réaction 3 La concentration de CLO est doublée₂ de la réaction 1, tandis que la concentration d'OH^- Reste constant.

Proportion entre les vitesses des réactions 3 et 1:

(8.28 x 10^-4 M · Min^-1) / (2.07 x 10^-4 M · Min^-1) = 4 (2²)

Et la proportion de [CLO₂] entre les réactions 3 et 1 est égal à:

(0,024 mol / L) / (0,012 mol / L) = 2^et

L'exposant 'et' représente l'ordre de la réaction concernant le réactif CLO₂.

Comparaison des proportions:

2² = 2^et

4 = 2^et

y = 2

Par conséquent, la réaction est deuxième par rapport au réactif CLO₂.

L'expression de la loi de vitesse sera alors:

Vitesse de réaction = k · [CLO₂]]²· [Oh^-]]

Calcul de K

Encore une fois, nous pouvons calculer K à partir de l'expression précédente en utilisant l'une des données cinétiques pour les expériences. Nous utiliserons l'expérience 3:

K = (8.28 x 10^-4 M · Min^-1) / (0.024 m)² (0.012 m)

= 119.79 min^-1· M^-2

Les références

1. Whitten, Davis, Peck & Stanley. (2008). Chimie. (8e Ed.). Cengage Learning.
2. Wikipédia. (2020). Constante de vitesse de réaction. Récupéré de: dans.Wikipédia.org
3. Chemistry Texas A&M University. (s.F.). Cinétique: calculs d'échantillonnage. Récupéré de: Chem.tamu.Édu
4. Keith J. Lancé. (2020). Taux de réaction. Britannica Encyclopaedia. Récupéré de: Britannica.com
5. Helmestine, Anne Marie, Ph.D. (25 août 2020). Quelle est la constante constante en chimie? Récupéré de: Thoughtco.com
6. Clark Jim. (2013). Constantes de taux et l'équation d'Arrhenius. Récupéré de: Chemguide.co.ROYAUME-UNI