Concept de compression et formules, calcul, exemples, exercices

La effort de compression ou de compression C'est la force par unité de zone dont le résultat est de pousser, de resserrer ou de comprimer un objet, tendant à le raccourcir. Mathématiquement est:

E = f / a

Ici ET Dénot l'effort, F l'ampleur de la force et POUR La zone sur laquelle l'unité se trouve dans le système international si le Newton / M² O Pascal (PA). L'effort de compression est un effort normal, Parce que la force qui le produit est perpendiculaire à la zone sur laquelle il est exercé.

Figure 1. Les colonnes de l'Acropole d'Athènes sont soumises à une compression. Source: Pixabay.

Un tel effort peut comprimer l'objet ou au contraire, le resserrer et l'étirer, comme appliqué. Dans le cas de l'effort de compression, les forces s'appliquent dans la direction opposée pour exercer l'effet du resserrement et du raccourcissement de l'objet.

Une fois que les forces cessent, de nombreux matériaux reviennent à leurs dimensions d'origine. Cette propriété est connue sous le nom de élasticité. Mais même si cela se produit, la déformation élastique unitaire subie par un matériel soumise à un effort est:

Déformation unitaire = (taille finale - taille initiale) / taille initiale

La déformation peut être linéaire, superficielle ou volume, bien que la déformation unitaire manque d'unités. Cependant, les informations qu'elle fournissent est très importante, car il n'est pas la même de déformer une barre de 10 m de long dans 1 cm, pour déformer 1 cm d'une autre barre de 1 m de long.

Dans un matériau élastique, la déformation et l'effort sont proportionnels, conformes à la loi de Hooke:

Effort ∝ Déformation unitaire

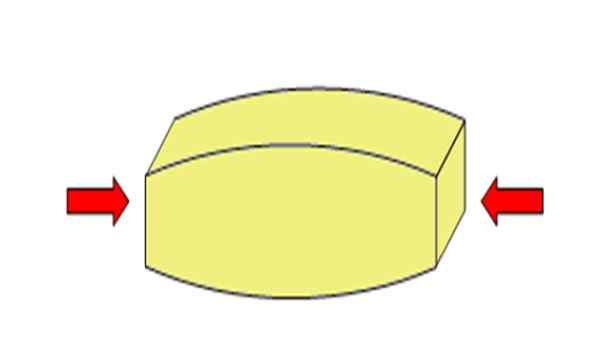Figure 2. L'effort de compression diminue la longueur de l'objet. Source: Wikimedia Commons. Adre-es [cc by-sa 4.0 (https: // CreativeCommons.Org / licences / by-sa / 4.0)].[TOC]

¿Comment calculer la compression?

L'effort de compression fait que les particules du matériau se rapprochent et plus, raccourcissant leur taille. Selon la direction dans laquelle l'effort est appliqué, il y aura un raccourcissement ou une réduction de l'une de ses dimensions.

Peut vous servir: modèle mécanique quantique de l'atome

Commençons par supposer une mince barre de longueur d'origine L,  à quel effort normal de grandeur est appliqué ET. Si l'effort est la compression, la barre subit une réduction de sa longueur, indiquée par δ. S'il s'agit de tension, la barre sera étendue.

Naturellement, le matériau dont l'élément est fabriqué est décisif dans sa capacité à soutenir les efforts.

Ces caractéristiques élastiques du matériau sont incluses dans la constante de proportionnalité susmentionnée. Il s'appelle module d'élasticité soit Jeune module et il est désigné comme et. Chaque matériau a un module d'élasticité, qui est déterminé expérimentalement par le biais de tests de laboratoire.

Dans cet esprit, l'effort ET Il s'exprime de manière mathématique comme ceci:

Effort ∝ Déformation unitaire

Enfin, pour établir cette condition comme une équation, une constante de proportionnalité est nécessaire pour remplacer le symbole de proportionnalité ∝ et le remplacer par l'égalité, comme ceci:

Effort = proportionnalité constante x déformation unitaire        

E = y. (Δ / L)

Le quotient (Δ / L) C'est la déformation unitaire, désignée comme ε et avec δ = Longueur finale - longueur initiale. De cette façon, l'effort ET Il reste comme:

E = y. ε

Étant donné que la déformation unitaire est sans dimension, les unités de ET sont les mêmes que ceux de ET: N / m² ou pa sur le système SI, livre / in² o psi dans le système britannique, ainsi que d'autres combinaisons de force et de zone, comme Kg / CM².

Module d'élasticité de différents matériaux

Les valeurs de et sont déterminées expérimentalement en laboratoire, dans des conditions contrôlées. Ensuite, le module d'élasticité des matériaux largement utilisés dans la construction et aussi celui des os:

Peut vous servir: vecteurs dans l'espace: comment graphiquement, applications, exercices

Tableau 1

Matériel	Module d'élasticité Y (PA) x 109
Acier	200
Fer	100
Laiton	100
Bronze	90
Aluminium	70
Marbre	cinquante
Granit	Quatre cinq
Béton	vingt
Os	quinze
Bois de pin	dix

Exemples

Les efforts de compression agissent sur diverses structures; La même chose qui est soumise à l'action de forces telles que le poids de chacun des éléments qui les composent, ainsi que les forces d'agents externes: vent, neige, autres structures et plus.

Il est habituel que la plupart des structures soient conçues pour résister aux efforts de toutes sortes sans se déformer. Par conséquent, il est nécessaire de prendre en compte l'effort de compression pour empêcher la pièce ou l'objet de perdre sa forme.

Les os du squelette sont également des structures soumises à divers efforts. Bien que les os leur soient résistants, lorsque la limite élastique est dépassée par accident, les fissures et les fractures proviennent.

Colonnes et piliers

Les colonnes et les piliers des bâtiments doivent être faits pour résister à la compression, sinon ils ont tendance à arché. Ceci est connu comme flexion latérale soit flambement.

Les colonnes (voir figure 1) sont des éléments dont la longueur est beaucoup plus élevée par rapport à la zone de sa section transversale.

Un élément cylindrique est une colonne lorsque sa longueur est égale ou supérieure à dix fois le diamètre de la section transversale. Mais si la section transversale n'est pas constante, son plus petit diamètre sera pris dans le but de classer l'élément comme une colonne.

Chaises et banques

Lorsque les gens prennent place dans des meubles tels que des chaises et des banques, ou ajoutent des objets sur le dessus, les jambes sont soumises à des efforts de compression qui ont tendance à réduire leur taille.

figure 3. Lorsqu'ils sont assis, les gens exercent un effort de compression sur la chaise, ce qui a tendance à raccourcir leur taille. Source: Pixabay.

Habituellement, les meubles sont conçus pour résister assez bien au poids et retourner à leur état naturel une fois retiré. Mais si un grand poids est placé dans des chaises ou des banques fragiles, les jambes donnent à la compression et à la rupture.

Peut vous servir: conducteurs électriques

Exercices

- Exercice 1

Vous avez une tige qui mesure à l'origine 12 m de longueur, à laquelle elle subit un effort de compression de telle sorte que sa déformation unitaire est de -0.0004. Quelle est la nouvelle longueur de tige?

Solution

À partir de l'équation donnée ci-dessus:

ε = (Δ / l) = - 0.0004

Ouais L_F C'est la longueur finale et L_soit la longueur initiale, puisque δ = L_F - L_soit  Tu as:

(L_F - L_soit) / L_soit = -0.0004

Donc: L_F - L_soit = -0.0004 x 12 m = -0.0048 m. Et finalement:

L_F  = (12 - 0.0048) M = 11.9952 m.

- Exercice 2

Une barre en acier solide, cylindrique, mesure 6 m de long et 8 cm de diamètre. Si la barre est soumise à une compression au moyen d'une charge de 90.000 kg, trouver:

a) L'ampleur de l'effort de compression dans Megapascal (MPA)

b) Combien la durée de la barre a-t-elle diminué?

Solution à

Le premier est la zone A de la section transversale de la barre, qui dépend de son diamètre D, résultant en:

A = π. D² / 4 = π. (0.08 m)² / 4 = 5.03 x 10^-3 m²

La force est immédiatement, à travers F = M.G = 90.000 kg x 9.8 m / s²= 882.000 N.

Enfin, l'effort moyen est calculé comme suit:

E = f / a = 882.000 n / 5.03 x 10^-3 m² = 1.75 x 10⁸ PA = 175 MPa

Solution B

L'équation de l'effort est maintenant utilisée, sachant que le matériau a une réponse élastique:

E = y. (Δ / L)

Le module Young en acier se trouve dans le tableau 1:

Δ = e.L / y = 6 m x 1.75 x 10⁸ PA / 200 X 10 ⁹ Pa = 5.25 x 10 ^-3 m = 5.25 mm.

Les références

1. Bière, f. 2010. Mécanique des matériaux. 5e. Édition. McGraw Hill.
2. Giancoli, D.  2006. Physique: principes avec applications. 6^Tth  Élégant. Prentice Hall.
3. Hibbeler, R.C. 2006. Mécanique des matériaux. 6e. Édition. Pearson Education.
4. Tippens, P. 2011. Physique: concepts et applications. 7e édition. McGraw Hill
5. Wikipédia. Stress (mécanique). Récupéré de: Wikipedia.org.