Compressibilité des solides, des liquides, des gaz, des exemples

La compressibilité d'une substance ou d'un matériau est le changement de volume qu'il subit lorsqu'il est soumis à un changement de pression. Habituellement, le volume diminue lors de l'application d'une pression sur un système ou un objet. Cependant, parfois l'inverse se produit: un changement de pression peut produire une explosion dans laquelle le système augmente le volume, ou lorsqu'un changement de phase a lieu.

Dans certaines réactions chimiques, cela peut se produire et dans les gaz aussi, car en augmentant la fréquence des collisions, les forces répulsives ont lieu.

Un sous-marin éprouve des forces de compression lorsqu'il est submergé. Source: Pixabay.com.

En imaginant à quel point il peut être facile ou difficile de comprimer un objet, vous devez considérer les trois états dans lesquels la question est normalement: solide, liquide et gazeux. Dans chacun d'eux, les molécules gardent certaines distances les unes des autres. Plus les liens qui unissent les molécules de substance qui se rapprochent de l'objet et de plus près sont difficiles, plus il sera difficile de provoquer une déformation.

Un solide a ses molécules très proches, et lorsqu'il essaie plus, les forces de répulsion apparaissent qui entravent la tâche. Par conséquent, on dit que les solides ne sont pas compressifs. Dans les molécules liquides, il y a plus d'espace, donc sa compressibilité est plus grande, mais le changement de volume nécessite généralement de grandes forces.

Donc les solides et les liquides sont à peine compressibles. Une très grande variation de pression serait nécessaire pour réaliser un changement appréciable dans les conditions normales de pression et de température normales. D'un autre côté, les gaz, car ils ont des molécules très espacées, sont facilement compressés et décompressés.

[TOC]

Compressibilité solide

Lorsqu'un objet est immergé dans un liquide par exemple, il exerce une pression sur l'objet dans toutes les directions. De cette façon, nous pouvons penser que le volume de l'objet diminuera, bien que dans la plupart des cas, ce ne sera pas appréciable.

La situation peut être vue dans la figure suivante:

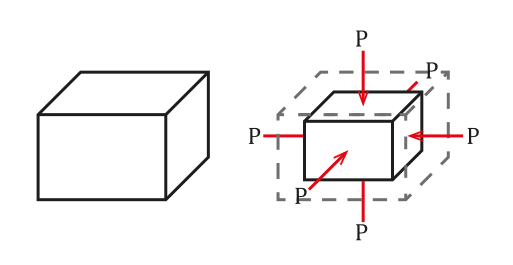La force exercée par le fluide sur l'objet submergé est perpendiculaire à la surface. Source: Wikimedia Commons.

La pression est définie comme une force par unité de zone, ce qui entraînera un changement de volume ΔV proportionnel au volume initial de l'objet V_soit. Ce changement de volume dépendra des qualités de même.

La loi de Hooke stipule que la déformation subie par un objet est proportionnelle à l'effort qui lui est appliqué:

Effort ∝ déformation

La déformation volumétrique connue par un corps est quantifiée par b la constante de proportionnalité requise, qui est appelée module volumétrique du matériau:

B = -seft / déformation unitaire

Peut vous servir: rayonnement thermique: propriétés, exemples, applications

B = -Δp / (Δv / v_soit)

Comme Δv / v_soit C'est une quantité sans dimension, car c'est le quotient entre deux volumes, le module volumétrique a les mêmes unités de pression, qui dans le système international sont Pascal (PA).

Le signe négatif indique la réduction attendue du volume, lorsque l'objet est suffisamment comprimé, c'est-à-dire que la pression augmente.

-Compressibilité d'un matériau

La valeur inverse ou réciproque du module volumétrique est connue sous le nom compressibilité Et il est indiqué avec les paroles k. Donc:

Ici k C'est le négatif du changement de volume fractionnaire dû à l'augmentation de la pression. Ses unités dans le système international sont l'inverse de l'AP, c'est-à-dire m² / N.

L'équation de B ou K si elle est préférée, s'applique aux solides et aux liquides. Le concept de module volumétrique est rarement appliqué aux gaz. Plus tard, un modèle simple est expliqué pour quantifier la diminution du volume qu'un réel gaz peut ressentir.

La vitesse du son et le module de compressibilité

Une application intéressante est la vitesse du son dans un support, qui dépend du module de compressibilité de la même chose:

Où c est la vitesse du son, b est le module volumétrique et ρ est la densité du milieu

Exercices résolus-exemples

-Exercice résolu 1

Une sphère en laiton solide dont le volume est 0.8 m³ Il tombe dans l'océan à une profondeur dans laquelle la pression hydrostatique est de 20 m plus grande que sur la surface. Quel changement connaîtra le volume de la sphère? Il est connu que le module de compressibilité en laiton est B = 35 000 MPa,

Solution

1 m Pa = 1 méga pascal = 1. dix ⁶ Pennsylvanie

La variation de pression par rapport à la surface est dp = 20 x 10 ⁶ Pennsylvanie. En appliquant l'équation donnée pour B, vous avez:

B = -Δp / (Δv / v_soit)

Donc:

Ensuite:

Δv = -5.71.dix ^-4 x 0.8 m³ = -4.57 x 10^-4 m³

La différence de volume peut avoir un signe négatif lorsque le volume final est inférieur au volume initial, donc ce résultat est d'accord avec toutes les hypothèses que nous avons faites jusqu'à présent.

Le module de compressibilité si élevé, indique qu'un grand changement de pression est nécessaire pour que l'objet subisse une diminution du volume appréciable.

-Exercice résolu 2

Mettre l'oreille contre les voies ferrées est connu lorsqu'un de ces véhicules s'approche au loin. Combien de temps dure le son lorsque vous voyagez à travers un rail en acier si le train est à 1 km de distance?

Peut vous servir: conservation de l'élan linéaire: principe, exemples, exercices.

Données

Densité d'acier = 7.8 x 10 ³ kg / m3

Module de compressibilité en acier = 2.0 x 10 ^onze Pennsylvanie.

Solution

Compressibilité des liquides

Le module de compressibilité B calculé ci-dessus est également appliqué aux liquides, bien qu'un grand effort soit généralement nécessaire pour produire une diminution appréciable du volume. Mais les liquides peuvent se développer ou se contracter lorsqu'ils chauffent ou se refroidissent, et aussi s'ils sont découragés ou sous pression.

Pour l'eau dans des conditions de pression et de température standard (0 ºC et une atmosphère de pression environ ou 100 kPa), le module volumétrique est de 2100 MPa. C'est-à-dire environ 21000 fois la pression atmosphérique.

Par conséquent, dans la plupart des applications, les liquides sont généralement considérés comme incompressibles. Cela peut être vu immédiatement avec une application numérique.

-Exercice résolu 3

Trouvez la diminution fractionnaire du volume d'eau lorsqu'il est soumis à une pression de 15 MPa.

Solution

Compressibilité dans les gaz

Les gaz, comme expliqué ci-dessus, fonctionnent un peu différemment.

Savoir quel volume ils ont n graphiques d'un gaz donné lorsqu'il est maintenu confiné à une pression P et à une température T, L'équation d'État est utilisée. Dans l'équation de l'État pour un gaz idéal, où les forces intermoléculaires ne sont pas prises en compte, le modèle le plus simple indique que:

P.V_idéal = n. R. T

Où r est la constante des gaz idéaux.

Des changements de volume de gaz peuvent être effectués à une pression constante ou à une température constante. Par exemple, en gardant la température constante, la compressibilité isotherme κ_T est:

Au lieu du symbole «delta» qui a été utilisé avant de définir le concept pour les solides, pour un gaz, il est décrit avec dérivé, dans ce cas dérivé partiel par rapport à P, en maintenant constant T.

Donc B_T Le module de compressibilité isotherme est:

 B_T = P

Et le module adiabatique BU-compressibilité B est également important_adiabatique, Pour lequel il n'y a pas de flux de chaleur entrant ou sortant.

B_adiabatique = γp

Où γ est le coefficient adiabatique. Avec ce coefficient, vous pouvez calculer la vitesse du son dans l'air:

-Exercice résolu 4

En appliquant l'équation précédente, trouvez la vitesse du son dans l'air.

Données

Le module de compressibilité de l'air adiabatique est de 1,42 × 10⁵ Pennsylvanie

La densité de l'air est 1.225 kg / m³ (à la pression atmosphérique et 15 ºC)

Solution

Le facteur de compressibilité Z

Au lieu de travailler avec le module de compressibilité, en tant que changement d'unité de volume en raison du changement de pression, le facteur de compressibilité du gaz réel, Un concept différent mais illustratif sur la façon dont le gaz réel se compare au gaz idéal:

Peut vous servir: Théorie ondulée de la lumière: explication, applications, exemples

P . V_réel = Z. R. T

Où z est la consultation de la compressibilité du gaz, qui dépend des conditions dans lesquelles il est, étant généralement fonction de la pression P et de la température T, en étant capable de s'exprimer comme:

Z = f (p, t)

Dans le cas d'un gaz idéal z = 1. Pour les gaz réels, la valeur Z augmente presque toujours avec la pression et diminue avec la température.

En augmentant la pression, les molécules gazeuses entrent plus fréquemment et les forces répulsives entre elles augmentent. Cela peut entraîner une augmentation du volume du gaz réel, donc z> 1.

D'un autre côté, pour réduire les pressions, les molécules sont libres de se déplacer et les forces d'attraction prédominent. Dans ce cas, z < 1.

Pour le cas simple de 1 mol de gaz n = 1, si les mêmes conditions de pression et de température sont maintenues, en divisant le terme, les équations précédentes sont obtenues:

Il est conclu que:

V_réel = Z v_idéal

-Exercice résolu 5

Il y a un gaz réel à 250 ºK et 15 atm de pression, qui a un volume molaire 12% inférieur à celui calculé par l'état des gaz idéaux. Si la pression et la température restent constantes, trouvez:

a) Le facteur de compressibilité.

b) le volume molaire de gaz réel.

c) Quel type de forces prédomine: attrayant ou repoussant?

Solution

a) Si le volume réel est de 12% inférieur à l'idéal, cela signifie que:

V_réel = 0.88 V_idéal

Par conséquent, pour 1 mole de gaz, le facteur de compressibilité est:

Z = 0.88

b) Choisir la constante des gaz idéaux avec les unités appropriées pour les données fournies:

R = 0,082 L.atm / mol.K

Le volume molaire est calculé en nettoyant et en remplaçant les valeurs:

c) Les forces attractives prédominent, car z est inférieur à 1.

Les références

1. Atkins, P. 2008. Chimie physique. Pan -American Medical Editorial. 10 - 15.
2. Giancoli, D.  2006. Physique: principes avec applications. 6^e. Ed Prentice Hall. 242 - 243 et 314-15
3. Mott, R.  2006. Mécanique des fluides. Pearson Education.13-14.
4. Rex, un. 2011. Fondamentaux de la physique. Pearson Education. 242-243.
5. Tipler, P. (2006) Physique de science et de technologie. 5e ed. Volume 1. Éditorial Revered. 542.