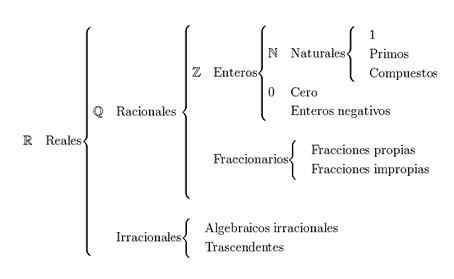
Classification des nombres réels

La principale Classification des nombres réels Il est divisé en nombres naturels, nombres entiers, nombres rationnels et nombres irrationnels. Les nombres réels sont représentés avec la lettre R.

Les nombres réels se réfèrent à la combinaison de groupes de nombres rationnels et irrationnels. Pour former ces groupes, des nombres naturels et des nombres entiers sont nécessaires.

Il existe de nombreuses façons dont les différents nombres réels peuvent être construits ou décrits, variant de formes plus simples aux formes plus complexes, selon le travail mathématique que vous souhaitez effectuer.

Comment les vrais nombres sont-ils classés?

- Nombres naturels

Les nombres naturels sont représentés par la lettre (n) et sont ceux utilisés pour compter (0,1,2,3,4 ...). Par exemple "il y a quinze Rosas dans le jardin »,« la population du Mexique est de 126 des millions de personnes "ou" la somme de deux et deux est quatre". Il convient de noter que certaines classifications incluent 0 comme nombre naturel et d'autres non. 

Deux enfants faisant une somme de deux nombres naturels.

Les nombres naturels n'incluent pas ceux qui ont une partie décimale. Par conséquent, «la population du Mexique est de 126.2 des millions de personnes "ou" fait une température de 24.5 Celsius Degrees »Les nombres naturels ne pouvaient pas être considérés.

En langue courante, comme les écoles primaires, les nombres naturels peuvent être appelés nombres comptables pour exclure les entiers négatifs et zéro.

Les nombres naturels sont les bases avec lesquelles de nombreux autres ensembles de nombres peuvent être construits par extension: nombres entiers, nombres rationnels, nombres réels et nombres complexes, entre autres.

Les propriétés des nombres naturels, telles que la divisibilité et la distribution des nombres primaires, sont étudiées en théorie des nombres. Les problèmes liés au comptage et à l'ordre, tels que les énumérations et la partition, sont étudiés dans le combinatoire.

Ils ont plusieurs propriétés, telles que: somme, multiplication, soustraction, division, etc.

Peut vous servir: science contemporaine

Nombres ordinaux et cardinaux

Les numéros naturels peuvent être ordinaux ou cardinaux.

Les numéros cardinaux seraient ceux qui sont utilisés comme nombres naturels, comme mentionné ci-dessus dans les exemples. "Ont deux Cookies "," Je suis le père de trois enfants »,« la boîte comprend deux crèmes cadeaux ". 

Les ordinaux sont ceux qui expriment l'ordre ou indiquent une position. Par exemple, dans une course, l'ordre d'arrivée des coureurs est répertorié par le vainqueur et terminant le dernier qui est venu sur la ligne d'arrivée.

De cette façon, il sera dit que le vainqueur est le "premier", le prochain "deuxième", le prochain "troisième" et ainsi de suite jusqu'au dernier. Ces chiffres peuvent être représentés par une lettre en haut à droite pour simplifier l'écriture (1er, 2e, 3e, 4e, etc.).

- Numéros entiers

Les nombres entiers sont composés de ces nombres naturels et de leurs opposés, c'est-à-dire les nombres négatifs (0, 1, -1, 2, -2, 50, -50 ...). Comme les nombres naturels, ceux-ci n'incluent pas ceux qui ont une partie décimale.

L'exemple de nombres entiers serait "la moyenne 30e en Allemagne", "Je suis resté à 0 en atteignant la fin du mois", "pour descendre au sous-sol, vous devez marquer le bouton de l'ascenseur" de l'ascenseur ".

À son tour, les nombres entiers ne peuvent pas être écrits avec un composant fractionnaire. Par exemple, des nombres comme 8.58 ou √2 ne sont pas des nombres entiers.

Les nombres entiers sont représentés par la lettre (z). Z est un groupe sous-marin de nombres rationnels Q, qui à leur tour forment le groupe de nombres N réels. Comme les nombres naturels, Z est un groupe comptable infini.

Les entiers forment le plus petit groupe et le plus petit ensemble de nombres naturels. Dans la théorie des nombres algébriques, les nombres entiers sont parfois appelés irrationnels pour les distinguer des entiers algébriques.

Il peut vous servir: Projet de recherche: Parties, comment il est élaboré et exemple

- Nombres rationnels

L'ensemble des nombres rationnels est représenté par la lettre (Q) et inclut tous ces nombres qui peuvent être écrits comme une fraction de nombres entiers.

Autrement dit, cet ensemble comprend des nombres naturels (4/1), des nombres entiers (-4/1) et des nombres décimaux exacts (15,50 = 1550/100).

La distribution de 1/6 de fromage est un nombre rationnel.

L'expansion décimale d'un nombre rationnel se termine toujours après un nombre fini de chiffres (par exemple 15,50) ou lorsque la même séquence finie de chiffres commence à être répétée encore et encore (par exemple 0,345666666666666…). Par conséquent, dans l'ensemble des nombres rationnels, les nombres sont inclus. journaux purs ou journaux mixtes.

De plus, toute décimale répétée ou terminale représente un nombre rationnel. Ces déclarations sont vraies non seulement pour la base 10, mais aussi pour tout autre numéro de base.

Un nombre réel qui n'est pas rationnel est appelé irrationnel. Les nombres irrationnels incluent √2, π et e, par exemple. Étant donné que l'ensemble des nombres rationnels est engourdis et que le groupe de nombres réels n'est pas engourdable, on peut dire que presque tous les nombres réels sont irrationnels.

Les nombres rationnels peuvent être officiellement définis comme des classes d'équivalence de paires entières (p, q) de sorte que q ≠ 0 ou la relation équivalente définie par (p1, q1) (p2, q2) uniquement si p1, q2 = p2q1.

Les nombres rationnels, ainsi que la somme et la multiplication, forment des champs qui composent les nombres entiers et sont contenus par n'importe quelle branche contenant entier.

- Nombres irrationnels

Les nombres irrationnels sont tous des nombres réels qui ne sont pas des nombres rationnels; Les nombres irrationnels ne peuvent pas être exprimés en fractions. Les nombres rationnels sont les nombres composés de fractions de nombres entiers.

En conséquence du test du chanteur qui dit que tous les nombres réels sont non nulles et que le rationnel s'ils sont des chiffres, on peut conclure que presque tous les nombres réels sont irrationnels.

Peut vous servir: trajectoire et déplacement

Lorsque le rayon de deux segments de ligne est un nombre irrationnel, on peut dire que ces segments de ligne sont incommensurables; ce qui signifie qu'il n'y a pas une longueur suffisante pour que chacun d'eux puisse être «mesure» avec un entier particulier multiple de la même.

Parmi les nombres irrationnels se trouvent le rayon π d'un cercle de cercle à son diamètre, le nombre d'Euler (e), le nombre d'or (φ) et la racine carrée de deux; Encore plus, toutes les racines carrées des nombres naturels sont irrationnelles. La seule exception à cette règle est les carrés parfaits.

On peut observer que lorsque les nombres irrationnels sont exprimés de manière positive dans un système de chiffres, (comme les nombres décimaux) ne terminent pas et ne répétent pas.

Cela signifie qu'ils ne contiennent pas de séquence de chiffres, la répétition par laquelle une ligne de représentation est faite.

Simplification du nombre irrationnel pi.

Par exemple: la représentation décimale du nombre π commence par 3.14159265358979, mais il n'y a pas de nombre fini de chiffres qui peuvent représenter exactement π, et ils ne peuvent pas être répétés.

La preuve que l'expansion décimale d'un nombre rationnel doit se terminer ou répéter est différente de la preuve qu'une extension décimale doit être un nombre rationnel; Bien que basiques et un peu longs, ces tests font du travail.

Habituellement, les mathématiciens ne prennent généralement pas la notion de «fin ou répéter» pour définir le concept d'un numéro rationnel.

Les nombres irrationnels peuvent également être traités via des fractions non continues.

Les références

1. Classer les nombres réels. Récupéré du chilimath.com.
2. Entier naturel. Récupéré de Wikipedia.org.
3. Classification des nombres. Dututor a récupéré.com.
4. Récupéré de Wikipedia.org.
5. Nombre irrationnel. Récupéré de Wikipedia.org.