Il s'appelle Nombres importants à la quantité de chiffres contenant le Mante d'un nombre. Plus il y a de nombres, la quantité est connue avec la plus grande précision. Pour rappel, la mantea est la figure qui accompagne la puissance de 10 lorsque le nombre en notation scientifique est écrit.

Par exemple, prenons le numéro 0.00376, qui est écrit comme 3.76 x 10 ^-3. La mantea a 3.76 et le nombre a un total de 3 chiffres significatifs. Le numéro 0.129 a également 3 chiffres significatifs, tandis que 4.5 n'a que 2.

Figure 1. Les calculatrices scientifiques ne montrent jamais le nombre de chiffres significatifs d'une opération. Source: piqsels.

Et que se passe-t-il lorsque le nombre est entier? Cela signifie qu'il est connu avec toute précision possible, en d'autres termes, il a une précision infinie. Par exemple, en comptant les personnes, les animaux ou les objets tels que les livres et les téléphones, le résultat est un entier et un numéro précis.

Si nous disons que dans une salle de cinéma, il y a 110 personnes qui regardent un film, c'est le nombre exact, ni plus ni moins, et a 3 chiffres significatifs.

Des chiffres importants sont traités par certaines règles simples qui sont mémorisées avec un peu de pratique, comme nous le verrons alors.

[TOC]

Règles pour déterminer les chiffres significatifs d'un nombre

Règle 1

Les zéros précédents ne comptent pas comme une figure significative, donc 0.045 et 4.5 Ils ont les deux 2 chiffres significatifs, car ceux-ci commencent à être comptés à partir de la gauche et à partir du premier chiffre différent de zéro.

Règle 2

Les zéros postérieurs (à droite) au premier chiffre significatif comptent comme une figure significative (tant qu'il est justifié par la précision de l'instrument de mesure).

Enfin, les zéros qui sont au milieu sont également considérés comme un chiffre significatif.

Règle 3

Pour les nombres écrits en notation scientifique, tous les chiffres de Mantisa sont significatifs et l'exposant n'influence pas la précision.

Il peut vous servir: vitesse moyenne: formules, comment elle est calculée et résolue

Règle 4

Lorsque des opérations avec des décimales sont prises, par exemple en calculant des zones ou d'autres opérations similaires, le résultat doit avoir le même nombre de chiffres significatifs que le montant avec le nombre le plus bas de chiffres significatifs qui ont participé à l'opération. Cette règle est valable pour toute opération arithmétique.

Règle 5

Le nombre du nombre n'influence pas son nombre de chiffres significatifs.

Nous verrons immédiatement quelques exemples de ceci et de toutes les autres règles.

Exemples

Exemple 1

Trouvez le nombre de chiffres significatifs dans chacun de ces nombres.

a) 876

b) 1000.68

c) 0.00005026

d) 4.8

e) -6.99

Réponses

A) 876 a 3 chiffres significatifs.

b) 1000.68 a 6 chiffres significatifs, puisque les zéros dans le compte moyen comme tel.

c) à la place 0.0000005026 a 4 chiffres significatifs. Notez que les 5 zéros à gauche du 5 ne sont pas comptés comme une figure significative, plutôt sur le 0 entre 5 et 2 oui.

d) 4.8 a 2 chiffres significatifs.

e) -6.99 a 3 chiffres significatifs.

Exemple 2

Il est courant de prendre des mesures de mesures, telles que des bandes métriques, des montres, des thermomètres, des échelles, etc. Combien de chiffres importants devons-nous signaler les montants que nous mesurons de cette manière?

Répondre

Cela dépend de l'appréciation de l'instrument avec lequel il est mesuré. Prenons un exemple: mesurez le diamètre externe d'un tube, avec une règle graduée et avec Vernier ou King's Foot.

Le Vernier est un instrument qui mesure les longueurs très précisément car elle a une petite échelle, appelée vernier, ce qui permet une plus grande finesse, pour ainsi dire, lors de la mesure.

C'est plus précis qu'une règle graduée car avec lui, nous pouvons apprendre des chiffres plus importants d'une certaine longueur.

C'est pourquoi cela n'a aucun sens de signaler un périmètre de, disons, 35.88 cm Si nous le mesurons avec du ruban à mesurer, car cet instrument n'est pas suffisamment précis pour signaler autant de chiffres significatifs.

Peut vous servir: statique: histoire, quelles études, applications, lois

L'appréciation du ruban à mesurer est donnée par:

Pour un ruban à mesurer ou une règle de millimètre, a = 1 mm, qui est le dixième d'un centimètre. Le périmètre mesuré avec du ruban à mesurer doit être signalé comme 35.9 cm.

Exemple 3

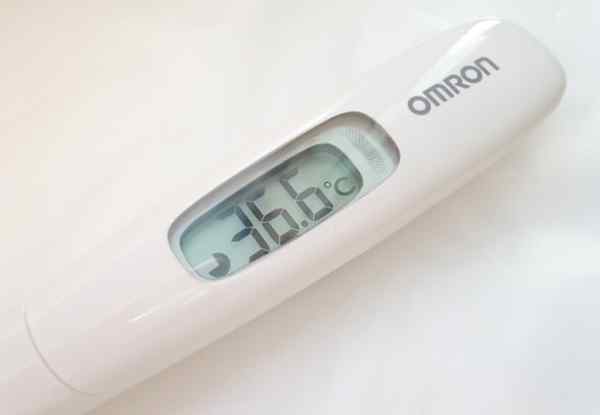
Combien de chiffres importants la lecture fait avec le thermomètre numérique a?

Répondre

Le thermomètre de la figure offre des lectures de température à trois chiffres. Cependant, dans la mesure montrée, 36.6 ºC, seuls les deux premiers chiffres de gauche à droite sont précis, car la décimale est affectée par l'erreur d'appréciation de l'instrument, qui est généralement indiqué à l'arrière de la même ou dans son manuel d'opérations.

La chose habituelle pour le type d'instrument numérique indiqué est une erreur de 0 appréciation.1 ºC. Cela suffit pour être sûr qu'il n'y a pas de fièvre.

Figure 2. Thermomètre numérique dont les lectures sont 3 chiffres significatifs. Source: pxhere.

Règles aux nombres ronds

Lorsqu'une calculatrice est utilisée pour effectuer des calculs avec des mesures obtenues, il n'est pas correct de donner le résultat en utilisant tous les chiffres qui apparaissent à l'écran.

Seuls ceux qui se connaissent précisément sont conservés, car seuls ceux-ci ont un vrai sens. Ensuite, il est nécessaire de compléter les résultats pour s'adapter au nombre de chiffres connues avec précision. Ces règles sont:

-Si le nombre qui suit le chiffre à conserver est égal ou supérieur à 5, À ce chiffre est ajouté 1.

Par exemple, en arrondissant 3.786 Pour avoir deux décimales, nous voulons conserver les chiffres jusqu'à 8. Puisque le nombre qui suit (6) est supérieur à 5, le 8 devient 8 + 1 = 9 et le nombre reste 3.79.

-Lorsque le nombre suivant le chiffre à conserver est Moins de 5, Le chiffre est le même.

Peut vous servir: Joule Effet: explication, exemples, exercices, applications

Si nous voulons le tour 1.27924 Pour avoir seulement 3 décimales, ceci est réalisé en atteignant 9, qui est suivi par un 2. Comme le 2 est inférieur à 5, ces décimales disparaissent et le nombre arrondi est 1.279.

Exercice résolu

Une table à manger a la forme et les dimensions indiquées dans la figure attachée. Il est invité à calculer sa zone en utilisant les règles d'opérations avec des chiffres importants.

Solution

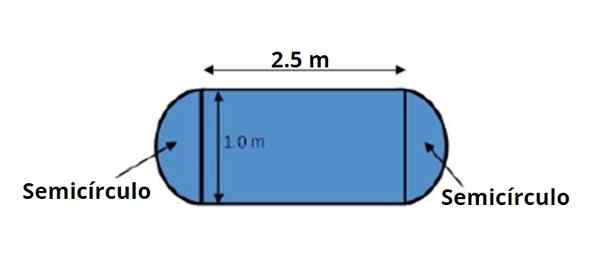figure 3. Un tableau a la forme et les dimensions indiquées sur la figure, notez que celles-ci sont connues avec deux chiffres significatifs. Source: F. Zapata.

La zone de la table peut être divisée en une zone rectangulaire centrale et deux demi-cercles, un de chaque côté, qui en font 1.

Nous appellerons₁ à la zone du rectangle, donné par:

POUR₁ = base × hauteur = 2.5 m x 1.0 m = 2.5m²

Pour sa part, la zone du cercle, qui équivaut à celle de 1 demi-cercle multiplié par 2 est:

POUR₂ = π × radio²

Le diamètre de l'un des demi-cercles est 1.0 m, donc le rayon est 0.50 m. Le diamètre pourrait également être utilisé directement pour calculer la zone, dans ce cas:

POUR₂ = (π × diamètre²) / 4

En tout cas:

POUR₂ = [π x (1.0 m)²] / 4 = 0.785398163 M²

Tous les chiffres offerts par la calculatrice ont été utilisés. Maintenant nous ajoutons à₁ déjà₂ Pour la zone totale de la table:

A = (2.5 + 0.785398163) M² = 3.285398163 M²

Comme les dimensions du tableau sont connues avec 2 chiffres significatifs, cela n'a aucun sens d'exprimer le résultat avec toutes les décimales données par la calculatrice, ce qui ne donne jamais le nombre de chiffres significatifs d'un résultat.

Ce qui doit être fait est de contourner la zone afin qu'il ait le même nombre de chiffres significatifs que les dimensions du tableau, c'est-à-dire 2. Par conséquent, le résultat final est rapporté comme ceci:

A = 3.3 m²

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
2. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique. Édité par Douglas Figueroa (USB).
3. Fisicab. Chiffres significatifs et arrondis. Récupéré de: Fisicalab.com.
4. Giancoli, D.  2006. Physique: principes avec applications. 6e. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1.