Propriétés de la charge ponctuelle et loi de Coulomb

Ongle Charge ponctuelle, Dans le contexte de l'électromagnétisme, c'est cette charge électrique de si petites dimensions, qui peuvent être considérées comme un point. Par exemple, les particules élémentaires qui ont la charge électrique, le proton et l'électron sont si petites que leurs dimensions peuvent être omises dans de nombreuses applications. Considérez qu'une charge est ponctuelle facilite le travail de calcul de ses interactions et de comprendre les propriétés électriques de la question.

Les particules élémentaires ne sont pas les seules qui peuvent être des charges spécifiques. Les molécules ionisées peuvent également être, les sphères chargées que Charles a utilisées. Coulomb (1736-1806) dans ses expériences et même la même terre. Tout peut être considéré comme des charges spécifiques, tant que nous les voyons à des distances beaucoup plus grandes que la taille de l'objet.

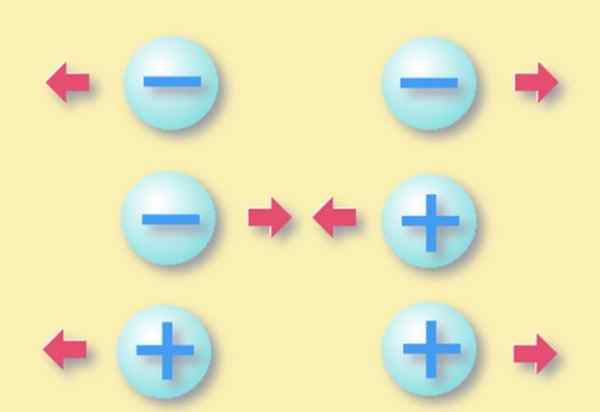
Figure 1. Les charges spécifiques du même signe sont repoussées, tandis que le signe inverse est attiré. Source: Wikimedia Commons.

Étant donné que tous les corps sont faits de particules élémentaires, la charge électrique est une propriété inhérente à la matière, tout comme la masse. Vous ne pouvez pas avoir un électron sans masse, et ni sans charge.

[TOC]

Propriétés

Pour autant que nous le sachions aujourd'hui, il existe deux types de charge électrique: positif et négatif. Les électrons ont une charge de type négative, tandis que les protons l'ont positif.

Des charges du même signe sont repoussées, tandis que le signe opposé est attiré. Ceci est valable pour tout type de charge électrique, soit ponctuel ou distribué sur un objet de dimensions mesurables.

De plus, des expériences minutieuses ont révélé que la charge de proton et l'électron ont exactement la même ampleur.

Un autre point très important à considérer est que la charge électrique est quantifiée. À ce jour, les charges électriques isolées n'ont pas été moins trouvées que la charge d'électrons. Tous en sont des multiples.

Enfin, la charge électrique est conservée. En d'autres termes, la charge électrique n'est pas créée ni détruite, mais elle peut être transférée d'un objet à un autre. De cette façon, si le système est isolé, la charge totale reste constante.

Peut vous servir: 21 événements importants de la physique

Unités de charge électrique

L'unité de charge électrique dans le système international des unités (SI) est Coulomb, abrégé avec une capitale C, en l'honneur de Charles à. Coulomb (1736-1806), qui a découvert la loi qui porte son nom et décrit l'interaction entre deux charges spécifiques. Plus tard, nous parlerons d'elle.

La charge électrique électronique, qui est la plus petite possible qui peut être isolée de nature, a une amplitude de:

et^- = 1.6 x 10 ^-16 C

Coulomb est une unité assez grande, donc les sous-cultiples sont souvent utilisés:

-1 mili C = 1 mc = 1 x 10^-3 C

-1 micro C = 1 μc = 1 x 10^-6 C

-1 nano c = 1 nc = 1 x 10^-9 C

Et comme nous l'avons mentionné précédemment, le signe de et^- C'est négatif. La charge de proton a exactement la même ampleur, mais avec un signe positif.

Les signes sont une question de convention, c'est-à-dire qu'il existe deux types d'électricité et il est nécessaire de les distinguer, donc l'un se voit attribuer le signe (-) et l'autre signe (+). Benjamin Franklin a fait cette désignation et a également énoncé le principe de conservation de la charge.

Pour le temps de Franklin, la structure interne de l'atome était encore inconnue, mais Franklin avait observé qu'une barre de verre frottée en soie était chargée électriquement, appelant ce type d'électricité positif.

Tout objet qui a été attiré par une telle électricité avait un signe négatif. Après la découverte de l'électron, il a été observé que la barre de verre chargée les a attirés, et c'est ainsi que la charge d'électrons était négative.

Coulomb Law pour des charges spécifiques

À la fin du XVIIIe siècle, Coulomb, ingénieur de l'armée française, a consacré beaucoup de temps à étudier les propriétés des matériaux, les forces qui agissent sur les poutres et la force de friction.

Mais la loi se souvient plus de la loi qui porte son nom et décrit l'interaction entre deux charges électriques spécifiques.

Peut vous servir: magnétisme: propriétés magnétiques des matériaux, utilisations

Laissez deux frais électriques q₁ et q₂. Coulomb a déterminé que la force entre eux, déjà hors d'attraction ou de répulsion, était directement proportionnelle au produit des deux charges, et inversement proportionnelle au carré de la distance entre eux.

Mathématiquement:

F∝ Q₁ . q₂ / r²

Dans cette équation, F représente l'ampleur de la force et r C'est la distance qui sépare les charges. L'égalité nécessite une constante de proportionnalité, qui est appelée constante électrostatique et est désignée comme k_et.

De cette façon:

F = k. q₁ . q₂ / r²

Coulomb a également constaté que la force était dirigée le long de la ligne qui rejoint les charges. Alors oui r C'est le vecteur d'unité le long de cette ligne, la loi de Coulomb en tant que vecteur est:

 Cette forme de la loi Coulomb s'applique uniquement à des charges spécifiques.

Application de la loi Coulomb 

Coulomb a utilisé un appareil appelé Équilibre de torsion Pour vos expériences. À travers elle, la valeur de la constante électrostatique pourrait être établie dans:

k_et = 8.99 x 10⁹ N m²/ C² ≈ 9.0 x 10⁹ N m²/ C²

Ensuite, nous verrons une application. Vous avez trois charges spécifiques qui_POUR, q_B et alors_C trouvé dans les positions indiquées sur la figure 2. Calculons la force nette sur q_B.

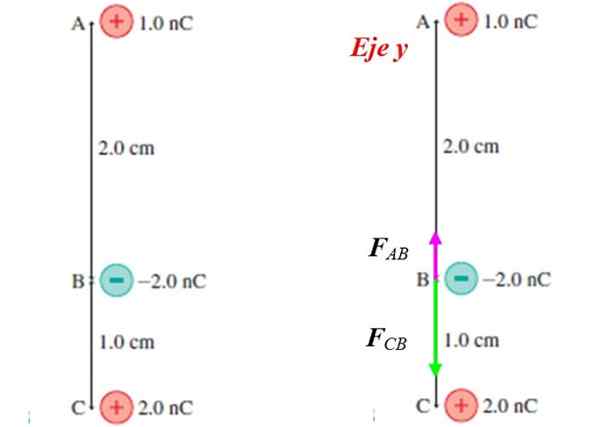Figure 2. La force sur la charge négative est calculée par la loi de Coulomb. Source: F. Zapata.

La charge q_POUR attire la charge q_B, Parce que ce sont des signes opposés. On peut en dire autant de q_C. Le diagramme corporel isolé est dans la figure 2 à droite, qui montre que les deux forces sont dirigées le long de l'axe vertical ou de l'axe Y, et ont des sens opposés.

La force nette sur la charge q_B est:

F_R = F_{UN B} + F_Cb (Principe de superposition)

Il ne reste que pour remplacer les valeurs numériques, en prenant soin d'écrire toutes les unités du système international (SI).

F_{UN B} = 9.0 x 10⁹ x 1 x 10^-9 x 2 x 10^-9 / (2 x 10^-2) ² N (+et) = 0.000045 (+et) N

F_Cb = 9.0 x 10⁹ x 2 x 10^-9 x 2 x 10^-9 / (1 x 10^-2) ² N (-et) = 0.00036 (-et) N

F_R = F_{UN B} + F_Cb = 0.000045 (+et) + 0.00036 (-et) N = 0.000315 (-et) N

Gravité et électricité

Ces deux forces ont la même forme mathématique. Bien sûr, ils diffèrent dans la valeur de la constante de proportionnalité et dans laquelle la gravité fonctionne avec les masses, tandis que l'électricité le fait avec des charges.

Peut vous servir: dynamique d'un système de particules: exemples, exercices

Mais l'important est que les deux dépendent de l'inverse du carré de la distance.

Il existe un type de masse unique et est considéré comme positif, donc la force gravitationnelle attire toujours, tandis que les charges peuvent être positives ou négatives. Par conséquent, les forces électriques peuvent être une attraction ou une répulsion, comme le cas.

Et nous avons ce détail qui dérive de ce qui précède: tous les objets en chute libre ont la même accélération, alors qu'ils sont près de la surface de la terre.

Mais si nous libérons un proton et un électron près d'un plan chargé, par exemple, l'électron aura une accélération beaucoup plus grande que celle du proton. De plus, les accélérations auront des sens opposés.

Enfin, la charge électrique est quantifiée, comme indiqué. Cela signifie que nous pouvons trouver des charges 2,3 ou 4 fois celles de l'électron - ou celle du proton-mais jamais 1.5 fois cette charge. Les masses ne sont plutôt pas des multiples d'une masse unique.

Dans le monde des particules subatomiques, la force électrique dépasse l'ampleur gravitationnelle. Cependant, à des échelles macroscopiques, la force de gravité est celle qui prédomine. Où? Au niveau des planètes, le système solaire, de la galaxie et plus.

Les références

1. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 5. Électrostatique. Édité par Douglas Figueroa (USB).
2. Giancoli, D. 2006. Physique: principes avec applications. 6e. Ed Prentice Hall.
3. Kirkpatrick, L. 2007. Physique: un regard sur le monde. 6e édition abrégée. Cengage Learning.
4. Chevalier, r. 2017. Physique pour les scientifiques et l'ingénierie: une approche stratégique. Pearson.
5. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. V 2.