Unités de capacité, formules, calcul, exemples

La Capacitance C'est la relation entre la charge d'un condensateur ou d'un entraîneur, mesurée en Coulomb, et son potentiel ou tension électrique, mesuré en volts. Il s'exprime dans les unités de Faradio (F), en l'honneur de Michael Faraday (1791-1867).

La capacité est également définie comme la propriété ou la capacité d'un condenseur ou d'un ensemble de condensateurs électriques, qui est mesuré par la quantité de charge électrique qui peut être stockée, séparément, par unité de changement du potentiel électrique.

Les lampes, ainsi que tout autre appareil électrique, doivent faire partie de leur fonctionnement à la capacité. Source: Pixabay.

Le terme capacité est introduit à la suite de la création d'un dispositif électrique appelé condensateur, inventé par le scientifique prussien Ewald Georg von Kleist, en 1745, et quel que soit le physicien néerlandais Pieter Van Musschenbroek.

Les condensateurs sont des dispositifs électriques qui stockent la charge électrique et le téléchargement instantanément. Cette propriété a été utilisée dans de nombreux appareils électriques, tels que la télévision, la radio, les lampes, l'ordinateur, entre autres dans la vie quotidienne.

[TOC]

Condensateur et capacité

Un condensateur ou un condensateur est composé de deux pilotes qui ont des charges égales et autrement. Les conducteurs sont appelés armures d'armure ou plaques de condenseur.

Une plaque est liée à la borne positive (+) d'une batterie, tandis que l'autre plaque est liée au négatif (-). Comme les plaques ont des charges égales et le signe opposé, la charge nette d'un condensateur est nulle (0).

La capacité est la relation entre la charge d'un conducteur ou des conducteurs qui forment un condensateur et la valeur de la différence de tension entre les plaques de condenseur.

Peut vous servir: réfrigérant Rosario

Unités et formules

La formule de capacité est la suivante:

C = Q / V

Où c est la capacité, q la charge (dont l'unité est le coulomb) et V  La tension (volt)

L'unité de capacité est la Faradio (F), qui équivaut à Coulomb / Voltio. Le Faradio est une très grande unité, donc le microphradium (µF) est utilisé, équivalent à 10^-6 farad; ou le pic de Faradio (PF), qui équivaut à 10^-12 farad.

Comment la capacité est-elle calculée?

Quelle sera la valeur de capacité d'un condensateur dont les plaques ont une charge de 5 · 10^-3 Coulomb et une différence de tension de 6 volts?

Application de la formule que nous résolvons:

C = Q / V

= (5 · 10^-3 Coulomb) / (6 volts)

= 8,33 · 10^-4  farad

Exemples

La formule de capacité varie en fonction du type de condensateur.

Condensateur de plaques parallèles

C = kε_soitPublicité

k est la constante diélectrique, qui a une valeur de 1 dans l'air et le vide. Pour cette raison, la formule est réduite à:

C = ε_soitPublicité

ε_soit C'est la constante diélectrique, dont la valeur est proche de 8 854 · 10^-12 F · m^-1, A est la zone ou la surface des plaques parallèles exprimées en m², alors que d La distance qui sépare les plaques parallèles.

Condensateur sphérique

C = 4πε_soitR

Où r est le rayon de la sphère en mètres.

Sphères concentriques

C = 4πε_soit / (1 / r₁ - 1 / r₂)

Condensateur de cylindre concentrique

C = 2πε_soitl / ln (r₂ / R₁)

Où l est la longueur des cylindres concentriques en mètres.

Exercices résolus

Condensateur à plaques plates parallèles

Quelle sera la capacité d'un condensateur ou d'un condensateur dans l'air avec une superficie de ses plaques de 3 cm² et séparé par une distance de 2 mm?

Peut vous servir: 12 exemples de bases chimiques

Nous avons la formule:

C = ε_soitPublicité

Et les données:

ε_soit = 8 854 x 10^-12 F · m^-1

A = 3 cm² (3 · 10^-4 m²)

D = 2 mm (2 · 10^-3 m)

Procéder à remplacer:

C = (8 854 · 10^-12 F · m^-1) (3 · 10^-4 m²) / (2 · 10^-3 m)

= 1 3281 · 10^-14 F

Condensateur ou condensateur en forme de sphère

Si la terre est considérée comme un condensateur sphérique avec un rayon (R) de 6.370 km: quelle sera la valeur de votre capacité?

Données:

C = 4πε_soitR

Π = 3 1416

ε_soit = 8 854 · 10^-12 F.m^-1

R = 6.370 km (6,37 · 10⁶ m)

Les valeurs de la formule de capacité sont à nouveau remplacées:

C = (4 · 3 1416) (8 854 · 10^-12 F · m^-1) (6,37 · 10⁶ m)

= 7,09 · 10^-8 F

= 709 µF

Combinaison de condensateurs

Les condensateurs ou condensateurs peuvent être combinés en série ou en parallèle.

Condensateurs de la série

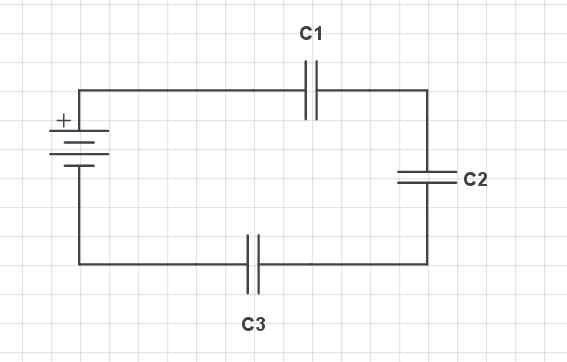Condensateurs de la série. Gabriel Bolívar Source via CircuitLab

L'image supérieure montre trois condensateurs de la série (C₁, C₂ et C₃), ainsi qu'une batterie avec ses bornes positives (+) et négatives (-). Ces condensateurs ont une série de caractéristiques par rapport à leur tension, leur charge et leur capacité.

Chute de tension (ΔV) chez les condensateurs

ΔV_t = Δv₁   +   ΔV₂   +    ΔV₃

La chute de tension totale dans un ensemble de condensateurs en série est égal à la somme des chutes de tension des condensateurs.

Fardeau  des condensateurs

Q_t = Q₁ = Q₂ = Q₃

La même quantité de charge circule à travers la série.

Capacité des condensateurs

La capacité équivalente des condensateurs en série présente la relation suivante:

1 c_égaliseur  = 1 / c₁  +   1 c₂   +   1 c₃

Condensateurs parallèles

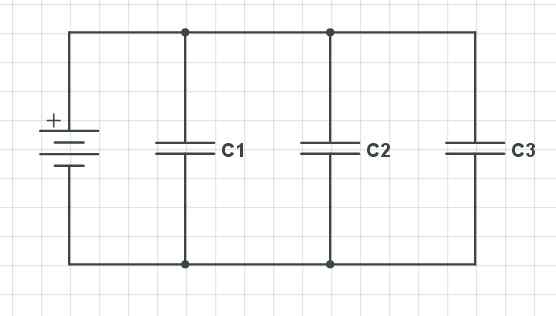Condensateurs parallèles. Gabriel Bolívar Source via CircuitLab.

Nous avons trois condensateurs disposés en parallèle (c₁, C₂ et C₃), qui maintient par rapport à la chute de tension, à la charge et à la capacité du comportement suivant:

Peut vous servir: alcènes

Baisse de tension dans les condensateurs

ΔV_t  = Δv₁  = Δv₂  = Δv₃

Dans les condensateurs parallèles, la chute de tension totale des condensateurs est la même que celle existante pour chacun des condensateurs.

Condensateurs

Q_t  = Q₁  +  Q₂  +  Q₃

Dans un système en parallèle, la charge totale des condensateurs est égale à la somme de la charge de tous les condensateurs.

Capacité des condensateurs

C_égaliseur  = C₁  +  C₂   +  C₃

Dans un système parallèle, la capacité équivalente d'entre eux est égale à la somme des capacités de tous les condensateurs.

Exemple d'exercice

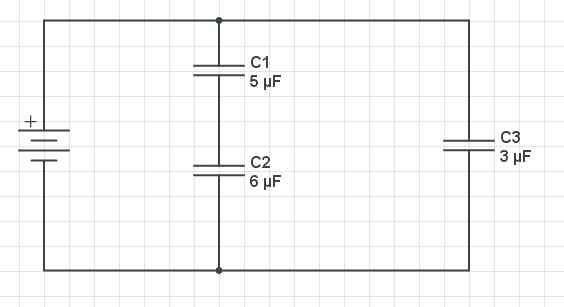Exemple de problème et de condensateurs parallèles. Gabriel Bolívar Source via CircuitLab.

Un schéma de trois condensateurs est illustré ci-dessus: C₁ et C₂ Ils sont disposés en série et ils sont en parallèle avec C₃. La capacité des condensateurs est la suivante: C₁ = 5 µf, C₂ = 6 µF et C₃ = 3 µF. Trouvez la capacité équivalente du circuit.

Le premier est la capacité équivalente de C₁ et C₂ qui sont en série.

1 c_Eq1,2 = 1 / c₁  +  1 c₂

1 c_Eq1,2 = 1/5 µF +1/6 µF

1 c_Eq1,2 = (11/30) µF

C_Eq1,2 = 30 µf / 11

= 2,72 µF

Les condensateurs 1 et 2 sont en parallèle avec C₃. Ainsi, la capacité équivalente de C₁, C₂ et C₃ est égal à c_Eq1,2 +  C₃.

C_Eq1,2,3 = 2,72 µF +3 µF

= 5,72 µF

Les références

1. SERAY, R. POUR. Et Jewett, J. W. (2009). Physique pour la science et l'ingénierie. 2ieme volume. Septième édition. Éditorial Cengage Learning.
2. Reddick, R et Halliday, D. (1965). Physique.  Partie 2. Deuxième édition en espagnol. Éditorial continental.POUR.
3. Étude. (22 avril 2015). Capacité: unités et formules. Récupéré de: étudier.com
4. Lumes Physique. (s.F.). Condensateurs en série et parallèle. Récupéré de: cours.Lumenarning.com
5. Les éditeurs d'Enyclopaedia Britannica. (2020). Capacitance. Récupéré de: Britannica.com