Équilibre de la matière ce que c'est, l'équation générale, les types

Il bilan matériel C'est le décompte des composants qui appartiennent à un système ou un processus à l'étude. Cet équilibre peut être appliqué presque à n'importe quel type de système, car il est supposé que la somme des masses de ces éléments doit rester constante pour différentes mesures des mesures.

Vous pouvez comprendre par composant des billes, des bactéries, des animaux, du bois, des ingrédients pour un gâteau; et dans le cas de la chimie, des molécules ou des ions, ou plus spécifiquement, des composés ou des substances. Ensuite, la masse totale des molécules qui entrent dans un système, avec ou sans réaction chimique doit rester constante; Tant qu'il n'y a pas de pertes de fuite.

En pratique, d'innombrables problèmes sont présentés qui peuvent affecter l'équilibre de la matière, en plus de prendre en compte divers phénomènes de matière et l'effet de nombreuses variables (température, pression, débit, agitation, taille des réacteurs, etc.).

Sur le papier, cependant, les calculs de l'équilibre de la matière doivent coïncider; c'est-à-dire que la masse des composés chimiques ne devrait pas disparaître à tout moment. Faire cet équilibre est analogue pour mettre un tas de rochers en équilibre. Si l'une des masses se déplace, tout s'effondre; Dans ce cas, cela signifierait que les calculs sont erronés.

Équation générale de l'équilibre des sujets

Dans chaque système ou processus, il faut d'abord définir quels sont leurs frontières. D'après eux, on connaîtra ce que les composés entrent ou partent. Il est pratique de le faire, surtout s'il existe plusieurs unités de processus à considérer. Lorsque toutes les unités ou sous-systèmes sont envisagés, il est question d'un bilan de matière générale.

Cet équilibre a une équation, qui peut être appliquée à tout système qui obéit à la loi de la conservation de masse. L'équation est la suivante:

Peut vous servir: chlorure de plomb: propriétés, structure, utilisations

E + g - s - c = a

Où e est la quantité de matière qui entre dans Au système; G est ce que je sais générer Si une réaction chimique se produit dans le processus (comme dans un réacteur); S c'est quoi sort du système; C est ce que je sais consommer, Encore une fois, s'il y a une réaction; Et enfin, c'est ce que je sais accumuler.

Simplification

Si dans le système ou le processus qui est étudié, il n'y a pas de réaction chimique, G et C valent zéro. Ainsi, l'équation reste:

E - s = a

Si le système est également pris en compte à l'état stationnaire, sans changements appréciables dans les variables ou les flux des composants, il est dit que rien ne s'accumule à l'intérieur. Par conséquent, il vaut zéro et l'équation finit par simplifier encore plus:

E = S

C'est-à-dire la quantité de matière qui entre est égale à celle qui sort. Rien ne peut être perdu ou disparaître.

D'un autre côté, s'il y a une réaction chimique, mais le système est à l'état stationnaire, G et C auront des valeurs et continueront d'être nul:

E + g - s - c = 0

E + g = s + c

Ce qui signifie que dans un réacteur, la masse des réactifs qui entrent et des produits qui génèrent dedans, est égal à la masse des produits et des réactifs qui sortent et des réactifs consommés.

Exemple de son utilisation: Fish in the River

Supposons que le nombre de poissons dans une rivière est étudié, dont les rives viennent représenter la frontière du système. Il est connu qu'en moyenne 568 poissons entrent par an, 424 sont nés (génèrent), 353 matrices (consommer) et 236 émigrer ou partir.

Application de l'équation générale alors vous avez:

568 + 424 - 353 - 236 = 403

Cela signifie qu'à 403 poissons, ils s'accumulent dans la rivière; c'est-à-dire par an la rivière enrichit plus de poisson. Si j'avais une valeur négative, cela signifierait que le nombre de poissons diminue, peut-être aux impacts environnementaux négatifs.

Il peut vous servir: force ionique: unités, comment la calculer, exemples

Gars

D'après l'équation générale, vous pouvez penser qu'il existe quatre équations pour différents types de processus chimiques. Cependant, l'équilibre de la matière est divisé en deux types selon un autre critère: le temps.

Équilibre différentiel

Dans l'équilibre de la matière différentielle, il y a le montant des composants dans un système à un moment ou une heure donnée. Ces quantités de masse sont exprimées avec des unités de temps et représentent donc des vitesses; Par exemple, kg / h, indiquant combien de kilomètres entrent, laissent, accumulent, génèrent ou consomment en une heure.

Pour qu'il y ait une masse (ou des flux volumétriques, avec la densité à portée de main), le système doit généralement être ouvert.

Équilibre intégral

Lorsque le système est fermé, comme avec les réactions effectuées dans des réacteurs intermittents (type de lot), les masses de ses composants s'intéressent généralement avant et après le processus; c'est-à-dire parmi les heures t initiales et finales.

Par conséquent, les quantités sont exprimées comme de simples masses et non des vitesses. Ce type d'équilibre est fait mentalement lorsqu'un mélangeur est utilisé: la masse des ingrédients qui entrent doit être égale à celle qui reste après le moteur.

Exemple d'exercice

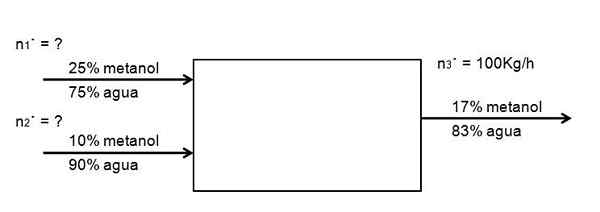
Il est souhaité diluer un débit d'une solution de méthanol à 25% dans l'eau, avec une autre concentration de 10%, plus diluée, de telle manière que 100 kg / h est généré à partir d'une solution de méthanol à 17%. Quelle part des deux solutions de méthanol, à 25 et 10%, doit entrer dans le système par heure pour y parvenir? Supposons que le système est à l'état stationnaire

Peut vous servir: saponification

Le diagramme suivant illustre la déclaration:

Diagramme d'écoulement pour la dilution de la dilution de la solution de méthanol. Source: Gabriel Bolívar.

Il n'y a pas de réaction chimique, donc la quantité de méthanol qui entre doit être égale à celle qui sort:

ET_Méthanol = S_Méthanol

0,25 N₁^· + 0,10 N₂^· = 0,17 N₃^·

Seule la valeur de n est connue₃^·. Les autres sont inconnus. Pour résoudre cette équation de deux inconnues, un autre équilibre est nécessaire: celui de l'eau. Ensuite, faire le même équilibre pour l'eau est:

0,75 N₁^· + 0,90 N₂^· = 0,83 N₃^·

La valeur de n est dégagée pour l'eau₁^· (Ça peut aussi être n₂^·):

n₁^· = (83 kg / h - 0,90N₂^·) / (0,75)

Remplacement alors n₁^· Dans l'équation de l'équilibre des matières pour le méthanol et la résolution de n₂^· Tu as:

0,25 [(83 kg / h - 0,90N₂^·) / (0,75)] + 0,10 n₂^· = 0,17 (100 kg / h)

n₂^· = 53,33 kg / h

Et pour obtenir n₁^· Il suffit de soustraire:

n₁^· = (100-53,33) kg / h

= 46,67 kg / h

Par conséquent, par heure, vous devez entrer dans le système de 46,67 kg de solution de méthanol à 25% et 53,33 kg de la solution à 10%.

Les références

1. Felder et Rousseau. (2000). Principes élémentaires des processus chimiques. (Deuxième édition.). Addison Wesley.
2. Fernández Germán. (20 octobre 2012). Définition de l'équilibre de la matière. Récupéré de: industrie.filet