Mesure de l'arc (géométrie), types d'arches, exemples

Il arc, En géométrie, c'est toute ligne incurvée qui relie deux points. Une ligne incurvée, contrairement à une ligne droite, est que la direction est différente à chaque point de même. L'opposé d'un arc est un segment, car il s'agit d'une section droite qui rejoint deux points.

L'arc qui est le plus fréquemment utilisé en géométrie est l'arc de circonférence. Les autres arches d'usage sont l'arc parabolique, l'arc elliptique et l'arc caténaire. La forme d'arc est également fréquemment utilisée dans l'architecture comme élément décoratif et élément structurel. C'est le cas des linteaux des portes et des fenêtres, ainsi que des ponts et des aqueducs.

Figure 1. L'arc-en-ciel est une ligne incurvée qui rejoint deux points à l'horizon. Source: Pixabay

[TOC]

L'arc et sa mesure

La mesure d'un arc est sa longueur, qui dépend du type de courbe qui relie les deux points et leur emplacement.

La longueur d'un arc circulaire est l'une des plus faciles à calculer, car la longueur ou le périmètre de l'arc complet d'un cercle est connu.

Le périmètre d'un cercle est deux pi fois votre radio: P = 2 π r. Sachant cela, si vous voulez calculer la longueur s d'une arche circulaire d'angle α (mesuré en radianes) et radio R, Une proportion est appliquée:

(s / p) = (α / 2 π)

Puis nettoyage s de l'expression précédente et de remplacement du périmètre p par son expression en fonction de la radio R, Tu as:

S = (α / 2 π) p = (α / 2 π) (2 π r) = α r.

C'est-à-dire que la mesure d'un arc circulaire est le produit de son ouverture angulaire par le rayon de l'arc circulaire.

Pour un arc d'une manière générale, le problème est plus compliqué, au point que les grands penseurs de l'antiquité ont affirmé que c'était une tâche impossible.

Il peut vous servir: quelles sont les expressions algébriques et qui sont les plus fréquentes?

Ce n'est que lorsque l'avènement du calcul différentiel et intégral en 1665, que le problème de mesure de tout arc a été résolu de manière satisfaisante. 

Avant l'invention du calcul différentiel, seules des solutions ont pu être trouvées grâce à l'utilisation de lines polygonales ou d'arcs de circonférence qui ont approché la véritable arche, mais ces solutions n'étaient pas exactes. 

Types d'arches

Du point de vue de la géométrie, les arches sont classées en fonction de la ligne incurvée qui rejoint deux points de l'avion. Il existe d'autres classifications selon son utilisation architecturale et sa forme.

Arc circulaire

Lorsque la ligne qui relie deux points de l'avion est un morceau de circonférence d'un certain rayon, il y a un arc circulaire. La figure 2 montre un arc circulaire de rayon R qui relie les points A et B.

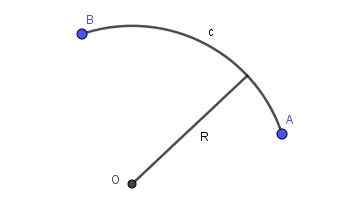Figure 2. Arc circulaire radio R qui relie les points A et B. Préparé par Ricardo Pérez.

Arc parabolique

La parabole est la trajectoire qui suit un objet qui a été jeté dans l'air sous forme oblique. Lorsque la courbe qui rejoint deux points est une parabole, il y a une arche parabolique comme celle illustrée à la figure 3.

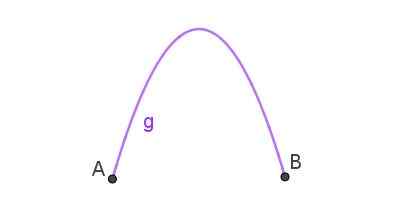figure 3. Arc parabolique qui relie les points A et B. Préparé par Ricardo Pérez.

C'est la forme qui adopte le jet d'eau qui sort d'un tuyau qui pointe. L'arc parabolique peut être observée dans les sources d'eau.

Figure 4. Arc parabolique formé par l'eau à partir d'une source à Dresde. Source: Pixabay.

Arc caténaire

L'arc caténaire est une autre arche naturelle. La caténaire est la courbe qui se forme naturellement lorsqu'une chaîne ou une corde est confortablement suspendue à deux points distincts.

Peut vous servir: quels sont les éléments d'un angle?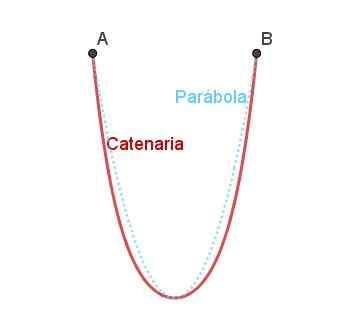 Figure 5. Arc caténaire et comparaison avec l'arc parabolique. Préparé par Ricardo Pérez.

Le caténaire est similaire à la parabole, mais il n'est pas exactement la même que ce qu'il peut être noté dans la figure 4.

L'arche en forme de caténaire inversée est utilisée dans l'architecture comme élément structurel de la forte résistance à la compression. En fait, il peut être démontré que c'est le type d'arc le plus résistant parmi toutes les formes possibles. 

Pour construire un arc caténaire solide, seule la forme d'une corde ou d'une chaîne est copiée, puis la forme copiée se tourne pour la reproduire dans la porte de la porte ou de la fenêtre.

Arc elliptique

Un arc est elliptique si la courbe qui relie deux points est un étirement ou un étirement d'ellipse. L'ellipse est définie comme le lieu géométrique des points dont la distance à deux points données ajoute toujours une quantité constante.

L'ellipse est une courbe qui apparaît dans la nature: c'est la courbe de la trajectoire de la planète autour du soleil, comme Johannes Kepler l'a démontré en 1609.

En pratique, une ellipse peut être dessinée en mettant deux entretoises sur le sol ou deux épingles sur du papier et en leur liant une corde. Ensuite, la corde est tendue avec le marqueur ou le crayon et la courbe est dessinée. Un morceau d'ellipse est une arche elliptique. L'animation suivante illustre comment l'ellipse est dessinée:

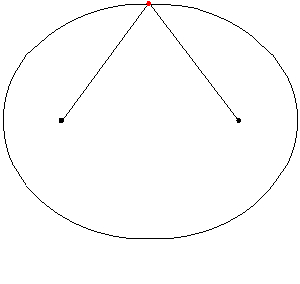Figure 5. Posen d'une ellipse à l'aide d'une corde tendue. Source: Wikimedia Commons

La figure 6 montre un arc elliptique qui relie les points G et H.

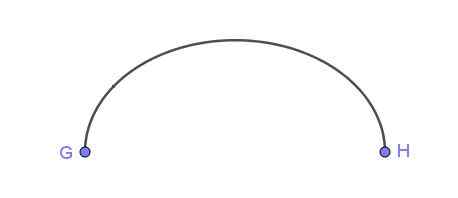Figure 6. Arc elliptique qui relie deux points. Préparé par Ricardo Pérez.

Exemples d'arches

Les exemples suivants se réfèrent à la façon de calculer le périmètre de certains arches spécifiques.

Peut vous servir: Nombres transcendants: quelles sont les formules, les exemples, les exercices

Exemple 1

La figure 7 montre une fenêtre terminée par un arc circulaire coupé. Les dimensions montrées sur la figure sont sur les pieds. Calculez la longueur de l'arc.

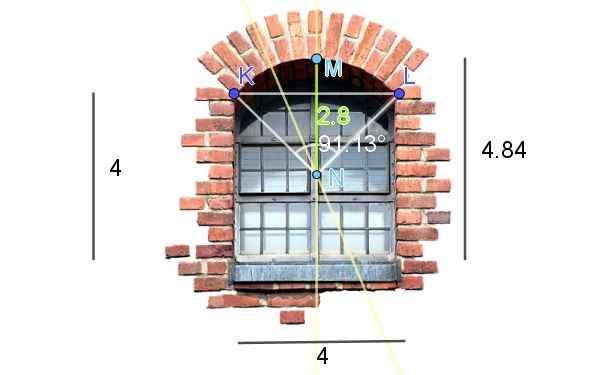Figure 7. Calcul de la longueur de l'arc circulaire d'une fenêtre. (Propres annotations - image de fenêtre en pixabay)

Pour obtenir le centre et le rayon de l'arc circulaire du linteau de la fenêtre, les constructions suivantes sont faites sur l'image:

-Le segment KL est dessiné et son MediaTrix est dessiné.

-Ensuite, le point le plus élevé du linteau est situé, que nous appelons m. Le segment KM est ensuite considéré et son MediaTrix est dessiné.

L'interception des deux médias est le point n et est également le centre de l'arc circulaire.

-Vous devez maintenant mesurer la longueur du segment NM, qui coïncide avec le rayon r de l'arc circulaire: r = 2.8 pieds.

-Pour connaître la longueur de l'arc en plus du rayon, l'angle qui forme l'arc. Qui peut être déterminé par deux méthodes, ou est mesuré avec un transporteur, ou calculé alternativement en utilisant la trigonométrie.

Dans le cas, l'angle qui forme l'arc est de 91,13º, qui doit être converti en rayons:

 91,13º = 91,13º * π / 180º = 1,59 radians

Nous calculons enfin la longueur s de l'arc à travers la formule S = α R.

S = 1,59 * 2.8 pieds = 4,45 pieds

Exemple 2

Trouvez la longueur de l'arc elliptique illustré à la figure 8, connu r et le semi-axe mineur s de l'ellipse.

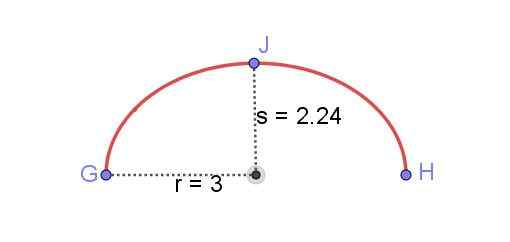Figure 8. Arc elliptique entre GH. Préparé par Ricardo Pérez.

Trouver la durée d'une ellipse a été longtemps l'un des problèmes les plus difficiles des mathématiques. Les solutions exprimées par les intégrales elliptiques peuvent être obtenues mais pour avoir une valeur numérique, ces intégrales en série de puissance doivent être élargies. Un résultat exact nécessiterait des termes infinis de ces séries.

Heureusement, le génie mathématique de l'origine hindoue Ramanujan, qui vivait entre 1887 et 1920, a trouvé une formule qui se rapproche de très précisément le périmètre d'une ellipse:

Périmètre d'une ellipse = π [3 (r + s) - √ ((3r + s) (r + 3s))]]

Le périmètre d'une ellipse avec r = 3 cm et s = 2.24 cm mesure 16,55 cm. Cependant, l'arc elliptique montré a la moitié de cette valeur:

Longueur arc elliptique gh = 8.28 cm.

Les références

1. Clemens S. 2008. Géométrie et trigonométrie. Pearson Education.
2. Garcia F. Procédures numériques en Java. Longueur d'une ellipse. Récupéré de: SC.Ehu.est
3. Géométrie dynamique. Arches. Récupéré de Geometriadinamica.est
4. Palissades. Ellipses et paraboles autour de nous. Récupéré de: Pizedas.com
5. Wikipédia. Arc (géométrie). Récupéré de: c'est.Wikipédia.com