Variation proportionnelle

Qu'est-ce que la variation proportionnelle?

La variation proportionnelle entre deux variables "x" et "y" a lieu lorsque, en multipliant l'une d'entre elles par une constante, l'autre est également multipliée ou divisée par la même constante. De nombreuses situations réelles peuvent être correctement décrites avec eux.

La proportionnalité entre les variables peut être directe ou inverse. Dans la proportionnalité directe, la relation est du type:

y = k ∙ x

Ou équivalent:

K = y / x

Où k est une constante appelée constante de proportionnalité soit rapport de proportionnalité. Notez que si "x" augmente, "Y" le fait dans la même proportion, et si "x" diminue, il "Y" sera également "Y". Lorsque la relation entre les variables est des graphiques, une ligne droite est obtenue qui passe par l'origine du système de coordonnées (voir l'exercice résolu plus tard).

La variation directe peut également se produire entre une variable et une puissance de l'autre, par exemple, "y" peut être directement proportionnel à x², X³ et donc.

D'un autre côté, en proportionnalité inverse, les variables sont liées par l'expression:

x ∙ y = k

Cette expression signifie que le produit des variables est une constante. Lorsque graphiquement la relation entre les variables est une hyperbole. De plus, si le produit d'une variable avec une puissance de l'autre est constant, il représente également un cas de proportionnalité inverse, par exemple:

X²∙ y = k; X³∙ y = k ..

Exemples

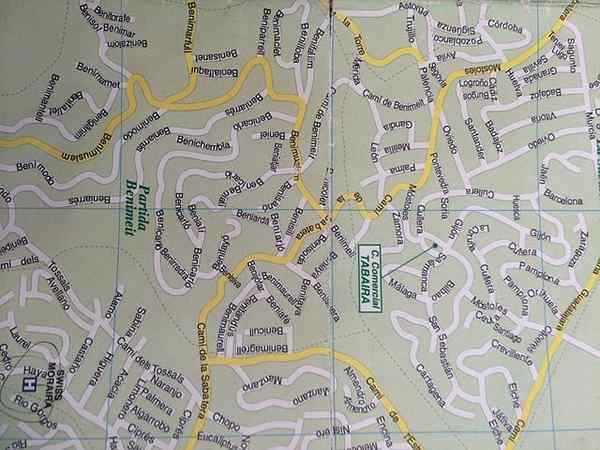Une application de variation proportionnelle est la disposition des cartes

De nombreuses lois de la physique et de la chimie sont exprimées mathématiquement en proportions. Par exemple, la force qui exerce un ressort et l'allongement de la même chose, la relation entre la pression et le volume dans un gaz à température constante, la période d'un pendule simple et la racine carrée de sa longueur et bien d'autres. Connaissant le modèle qui régit le phénomène, vous pouvez trouver votre comportement pour toute valeur des variables.

Peut vous servir: Théorème d'existence et d'unicité: démonstration, exemples et exercices

Et non seulement cela, ils s'appliquent également dans d'innombrables situations comme celles-ci:

• Passez le motif d'un vêtement d'une taille plus petite à une taille plus grande (ou vice versa).
• Dans les facteurs de conversion, pour passer d'une unité à l'autre, comme les kilomètres à des kilomètres, des gallons à des litres et plus.
• Calculez les ingrédients d'une recette pour 6 personnes connaissant l'exigence de 4 personnes.
• Déterminer le montant de certaines taxes conformément aux revenus obtenus.
• Dans le calcul de l'intérêt simple.
• Lorsque vous dessinez des avions à l'échelle.
• Lorsque vous devez calculer le prix d'une quantité de produits connaissant le prix unitaire.
• Dans la similitude des triangles.

Ensuite, en détail, il existe deux situations intéressantes où les variations proportionnelles s'appliquent:

Exemple 1

À l'échelle d'une ville, l'avenue Hermitage mesure 3.2 cm, étant sa véritable longueur de 400 m. D'un autre côté, la rue de La Fuente, qui mesure vraiment 180 m de long doit dessiner avec un accident vasculaire cérébral proportionnel. Quelle est la taille de la course?

La déclaration propose les informations complètes de l'avenue Ermita: laissez la longueur réelle de l'avenue et ℓ sa longueur sur l'avion, car la variation est de proportionnalité directe, elle doit:

L = k ∙ ℓ

À partir des données sur l'avenue Hermitage, vous pouvez connaître la valeur de la constante de proportionnalité K, mais avant qu'il ne soit nécessaire de laisser toutes les longueurs dans les mêmes unités:

3.2 cm = 0.032 m

Ensuite:

400 m = k ∙ 0.032 m

Par conséquent, la constante de proportionnalité est:

Peut vous servir: quels sont les éléments de la parabole? (Les pièces)

K = 400/0.032 = 12500

Maintenant, on sait que:

L = 12500 ∙ ℓ

Ce résultat est interprété comme suit: La longueur des rues de cette carte est 12500 fois plus petite que sa longueur réelle. Par conséquent, la ligne de la rue de La Fuente mesures:

ℓ = 180 m / 12500 = 0.0144 M = 1.44 cm

Exemple 2

Un analyste a le tableau des valeurs suivant pour les variables "x" et "y" obtenues expérimentalement et veut savoir si ces données correspondent à un modèle de variation proportionnelle directe ou une variation proportionnelle inverse.

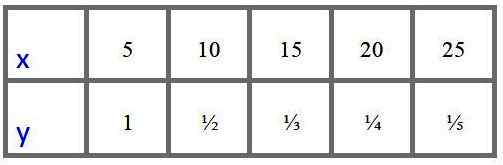
Que devriez-vous faire pour savoir?

En premier lieu, il est observé que lorsque «x» augmente, «y» diminue, il soupçonne donc une proportionnalité inverse, en tout cas, pour s'assurer que l'analyste a la possibilité d'évaluer si le quotient et / x est constant (proportionnel variation directe) ou si le produit x.et est constant (variation proportionnelle inverse).

Test avec la première option:

1 ÷ 5 = 0.2

½ ÷ 10 = 0.05

⅓ ÷ 15 = 0.022 ..

Il est conclu qu'il ne s'agit pas d'une variation proportionnelle directe, car le quotient et / x donne des valeurs différentes pour chaque couple de données.

Nous devons vérifier si le produit X ∙ est constant:

5 × 1 = 5

10 × ½ = 5

15 × ⅓ = 5

20 × ¼ = 5

25 × ⅕ = 5

Et comme le produit x ∙ y = 5, il est conclu que la variation est de proportionnalité inverse.

Ces informations servent à connaître des valeurs qui ne sont pas dans le tableau, par exemple, quelle serait la valeur de «y» lorsque x = 30?

De x ∙ y = 5, «y» est effacé et remplacé x = 30:

y = 5 / x

y = 5/30 = 1/6

Exercice résolu

Si un compteur de tissu coûte 6.75 $, et sachant que le prix est directement proportionnel au montant des mètres à acheter, trouvez:

Il peut vous servir: antidérivatif: formules et équations, exemples, exercices

a) L'expression algébrique qui relie les variables "prix à $" et "nombre de mètres de tissu".

b) Préparer un tableau des valeurs avec des prix de 3, 6, 9, 12, 15 et 18 mètres de tissu.

c) graphiquement les valeurs obtenues.

Réponds à

Soit "y" le prix variable "à $" et "x" la variable "quantité de mètres de tissu". Comme c'est directement proportionnel, vous devez:

y = k ∙ x

Pour x = 1 mètre, y = 6.75 $, donc k = 6.75 $ / mètre. Il s'agit du prix unitaire du tissu, le prix de tout autre tissu "x" est obtenu en multipliant par cette valeur, alors, l'expression algébrique recherchée est:

y = 6.75 ∙ x

Réponse b

Le tableau des valeurs à des prix à 3, 6, 9, 12, 15 et 18 mètres est:

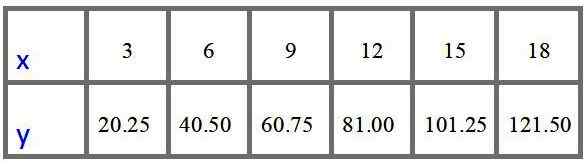
Réponse C

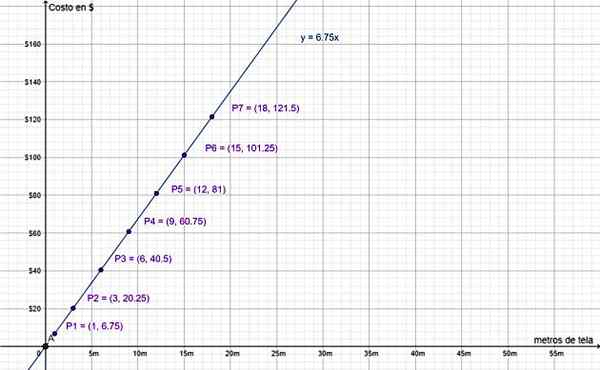
Enfin, le graphique des valeurs du tableau précédent corrobore qu'il s'agit d'une variation proportionnelle directe:

Le coût à $ et le montant des mètres de tissu sont directement proportionnels. Source: F. Zapata.

Notez que la valeur (0,0) est incluse, car la ligne y = 6.75 ∙ x passe par l'origine du système de coordonnées, comme expliqué précédemment. Cela a du sens, car ne pas faire d'achat équivaut à acheter 0 m de tissu, dont la valeur est 0 $.

Les références

1. Larson, R. 2012. Présculpture. 8e. Édition. Cengage Learning.
2. Secrétariat de l'éducation publique au Mexique. La variation proportionnelle. Récupéré de: PPS.K12.Ou.nous.
3. Stewart, J. 2007. Pré-calcul: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
4. Unam. Guides d'étude: Mathématiques I. Récupéré de: dirre.Unam.mx.
5. Zill, D. 2008. Pré-calcul avec avancées de calcul. 4e. Édition. McGraw Hill.