Triangle scalène

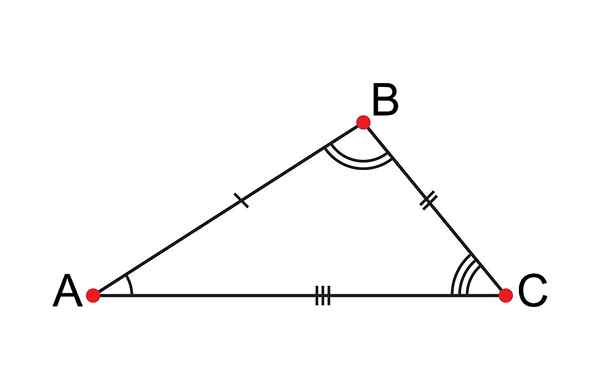
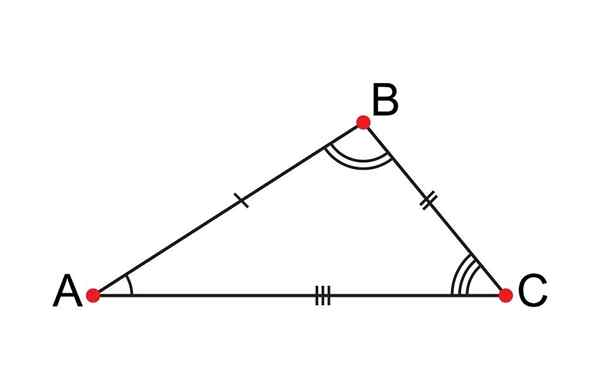Le triangle scalène a tous ses côtés inégaux

Qu'est-ce qu'un triangle scalène?

UN triangle scalène Il s'agit d'un polygone à trois faces, où tout le monde a des mesures ou des longueurs différentes; Pour cette raison, il a reçu le nom d'Escaleno, qui en latin signifie inégal.

Les triangles sont des polygones considérés comme les plus simples en géométrie, car trois côtés, trois angles et trois sommets se forment. Dans le cas du triangle scalène, pour avoir tous les différents côtés, cela implique que ses trois angles seront également.

Caractéristiques des triangles à l'échelle

Les triangles à l'échelle sont des polygones simples car aucun de ses côtés ou des angles n'a la même mesure, contrairement aux triangles isocèles et à l'équilibre.

Parce que tous leurs côtés et angles ont des mesures différentes, ces triangles sont considérés comme des polygones convexes irréguliers.

Selon l'amplitude des angles internes, les triangles scalène sont classés comme:

• Triangle rectangle scalène: Tous ses côtés sont différents. Un de ses angles est droit (90^soit) et les autres sont aigus et avec différentes mesures.
• Triangle de scalène obtus: Tous ses côtés sont différents et l'un de ses angles est obtus (> 90^soit).
• Triangle scalène acutangle: Tous ses côtés sont différents. Tous ses angles sont aigus (< 90^soit), Avec différentes mesures.

Une autre caractéristique des triangles scalène est que le fait de l'incohérence.

Composants / éléments

La médiane

C'est une ligne qui part du point médian d'un côté et atteint le sommet opposé. Les trois médiums assistent à un point appelé baricentro ou centroïde.

La bissectrice

C'est un semi-droit qui divise chaque angle en deux angles de mesure égale. Les bissecteurs d'un triangle s'accordent au point appelé incitateur.

Le MediaTrix

C'est un segment perpendiculaire au côté du triangle, qui provient au milieu de ce. Il y a trois MediaTrices dans un triangle et assister à un point appelé Circumcentro.

L'hauteur 

C'est la ligne qui va du sommet au côté opposé, et aussi cette ligne est perpendiculaire à ce côté. Tous les triangles ont trois hauteurs qui coïncident à un point appelé OrtoSenter.

Propriétés du triange de l'Escaleno

Les triangles à l'échelle sont définis ou identifiés car ils ont plusieurs propriétés qui les représentent, provenant des théorèmes proposés par les grands mathématiciens. Elles sont:

Angles internes

La somme des angles internes est toujours égal à 180^soit.

Somme des côtés

La somme des mesures de deux côtés doit toujours être supérieure à la mesure du troisième côté, A + B> C.

Côtés incongrus

Tous les côtés des triangles d'escalade ont des mesures ou des longueurs différentes; c'est-à-dire qu'ils sont incongrues.

Angles incongru

Étant donné que tous les côtés du triangle scalène sont différents, ses angles seront également. Cependant, la somme des angles internes sera toujours égale à 180 °, et dans certains cas, l'un de ses angles peut être obtus ou droit, tandis que dans d'autres tous ses angles seront aigus.

Peut vous servir: problèmes multiplicatifs pour les enfants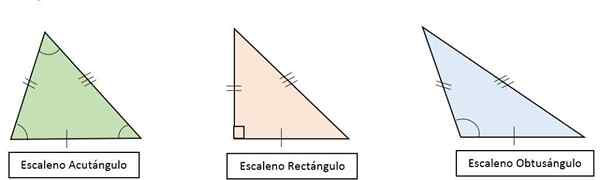 Types de triangles de scalele selon leurs angles

La hauteur, la médiane, la média et la bissector ne sont pas une coïncidence

Comme tout triangle, Escaleno a diverses lignes de lignes qui la composent, comme: Hauteur, Medium, MediaTrix et Bissector.

En raison de la particularité de ses côtés, dans ce type de triangle, aucune de ces lignes ne coïncidera en un seul.

Orocentro, Baricentro, Incentro et Circumcentro ne sont pas une coïncidence

Comme la hauteur, la médiane, la bissectrice et le média sont représentées par différents segments de lignes, dans un triangle scalène les points de rencontre - l'orthocentre, l'incentre et le barcenter de circoncentro se trouvent à différents points (c'est-à-dire qu'ils ne coïncident pas).

Selon que le triangle est acutangle, rectangle ou obtus, l'orthocentre a des emplacements différents:

pour. Si le triangle est acutangle, l'orthocentre sera à l'intérieur du triangle.

b. Si le triangle est rectangle, l'orthocentre coïncidera avec le sommet sur le côté droit.

c. Si le triangle est obtus, l'ootocentre sera à l'extérieur du triangle.

Hauteurs relatives

Les hauteurs sont relatives aux côtés.

Dans le cas du triangle scalène, ces hauteurs auront des mesures différentes. Chaque triangle a trois hauteurs relatives et pour les calculer, la formule Herón est utilisée.

Calcul du périmètre, surface, hauteur et côtés

Comment calculer le périmètre?

Le périmètre d'un polygone est calculé par la somme des côtés.

Comme dans ce cas, le triangle scalène a tous ses côtés avec une mesure différente, son périmètre sera:

P = côté à + côté b + côté c.

Comment calculer la zone?

Les triangles sont toujours calculés avec la même formule, multipliant la base par hauteur et divisant par deux:

Zone = (base _* H) ÷ 2

Dans certains cas, la hauteur du triangle scalène n'est pas connue, mais il existe une formule qui a été proposée par le mathématicien Herón, pour calculer la zone connaissant la mesure des trois côtés d'un triangle.

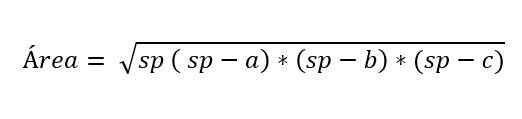
Où:

• A, B et C représentent les côtés du triangle.
• SP correspond au demi-périmètre du triangle, c'est-à-dire la moitié du périmètre:

sp = (a + b + c) ÷ 2

Dans le cas où seuls deux des côtés du triangle et l'angle qui se forment entre eux se trouvent, la zone peut être calculée en appliquant les raisons trigonométriques. Ainsi, vous devez:

Zone = (côté _* H) ÷ 2

Où la hauteur (h) est le produit d'un côté à travers l'angle opposé. Par exemple, pour chaque côté, la zone sera:

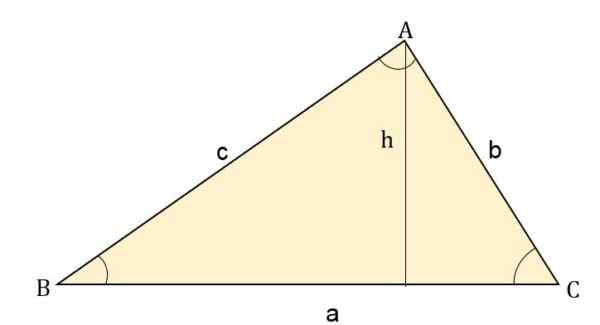
• Zone = (b _* c _* péché a) ÷ 2
• Zone = (a _* c _* péché b) ÷ 2.
• Zone = (a _* b _* Sen c) ÷ 2

Comment calculer la hauteur?

Comme tous les côtés du triangle scalène, ils sont différents, il n'est pas possible de calculer la hauteur avec le théorème de Pythagore.

De la formule Herón, qui est basée sur les mesures des trois côtés d'un triangle, la zone peut être calculée.

Peut vous servir: Notation factorielle: concept, exemples et exercices

La hauteur peut être claire à partir de la formule générale de la zone:

Formule pour calculer la hauteur d'un triangle scalène

Le côté est remplacé par la mesure des côtés A, B ou C.

Une autre façon de calculer la hauteur lorsque la valeur de l'un des angles est connue, consiste à appliquer les raisons trigonométriques, où la hauteur représentera un triangle cateto.

Par exemple, lorsque l'angle opposé est connu de la hauteur, il sera déterminé par le sein:

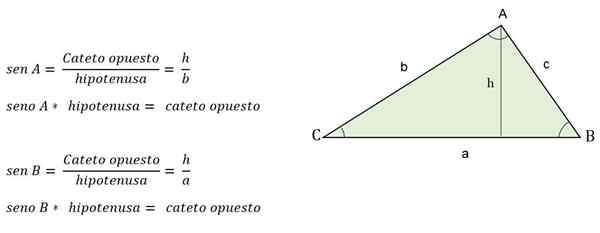Formule trigonométrique pour calculer la hauteur d'un triangle scalène

Comment calculer les côtés?

Lorsque vous avez la mesure des deux côtés et l'angle opposé à ceux-ci, il est possible de déterminer le troisième côté appliquant le théorème des cosenos.

Par exemple, dans un triangle ab, la hauteur par rapport au segment AC est dessinée. De cette façon, le triangle est divisé en deux triangles rectangulaires.

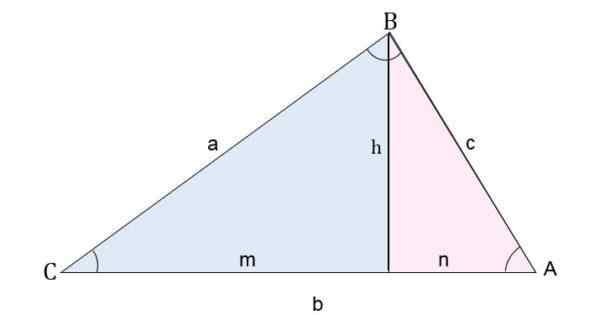Division d'un triangle scalène en deux rectangles pour calculer les côtés

Pour calculer le côté C (segment AB), le théorème de Pythagore pour chaque triangle est appliqué:

• Pour le triangle bleu, vous devez:

c² = H² + m²

Comme m = b - n, il est remplacé:

c² = H² + b² (B - n)²

c² = H² + b² - 2BN + N².

• Pour le triangle rose, vous devez:

H² = A² - n²

Il est remplacé dans l'équation précédente:

c² = A² - n² + b² - 2BN + N²

c² = A² + b² - 2BN.

Sachant que n = a _* cos c, est remplacé dans l'équation précédente et la valeur du côté C est obtenue:

c² = A² + b² - 2B_* pour _* COS C.

Par la loi des cosenos, les côtés peuvent être calculés comme suit:

• pour² = b² + c² - 2B_* c _* truc.
• b² = A² + c² - 2e_* c _* cos b.
• c² = A² + b² - 2B_* pour _* COS C.

Il y a des cas où les mesures des côtés du triangle ne sont pas connues, mais sa hauteur et les angles qui se forment dans les sommets. Pour déterminer la zone dans ces cas, il est nécessaire d'appliquer des raisons trigonométriques.

Connaissant l'angle de l'un de ses sommets, la catégorie est identifiée et la raison trigonométrique correspondante est utilisée:

Formule trigonométrique pour calculer les côtés d'un triangle scalène

Par exemple, le Cateto AB sera opposé à l'angle C, mais adjacent à l'angle a. Selon le côté ou la jambe correspondant à la hauteur, l'autre côté est éliminé pour obtenir la valeur de ce.

Exercices résolus

Premier exercice

Calculez la zone et une hauteur du triangle Escalano ABC, sachant que ses côtés sont:

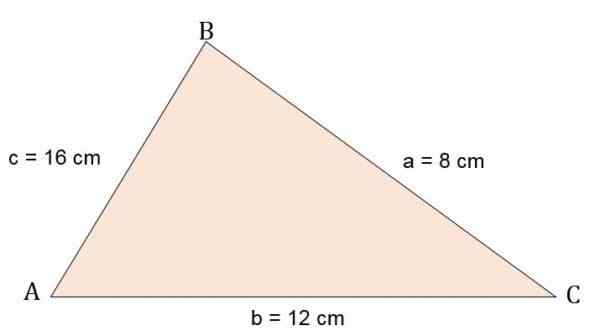
A = 8 cm.

B = 12 cm.

C = 16 cm.

Solution

Comme les données sont données les mesures des trois côtés du triangle scalène.

Parce que vous n'avez pas la valeur de la hauteur, la zone peut être déterminée en appliquant la formule Herón.

Le semi-périmètre est d'abord calculé:

sp = (a + b + c) ÷ 2

Sp = (8 cm + 12 cm + 16 cm) ÷ 2

sp = 36 cm ÷ 2

sp = 18 cm.

Maintenant, les valeurs de la formule d'Herón sont remplacées:

Peut vous servir: Fréquence absolue: formule, calcul, distribution, exemple Formule Herón

Connaître la zone peut être calculé la hauteur relative au côté B. De la formule générale, en le nettoyant:

Zone = (côté _* H) ÷ 2

46, 47 cm² = (12 cm _* H) ÷ 2

H = (2 _* 46,47 cm²) ÷ 12 cm

H = 92,94 cm² ÷ 12 cm

H = 7,75 cm.

Deuxième exercice

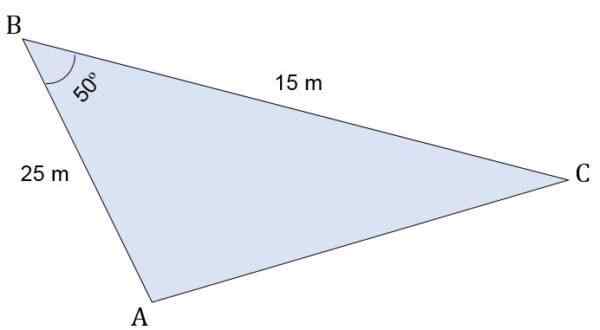
Compte tenu du triangle ABC Escalano, dont les mesures sont:

• Segment ab = 25 m.
• Segment BC = 15 m.

Dans le sommet B, un angle de 50º est formé. Calculez la hauteur par rapport au côté C, au périmètre et à la zone de ce triangle.

Solution

Dans ce cas, il y a deux mesures. Pour déterminer la hauteur, il est nécessaire de calculer la mesure du troisième côté.

Comme l'angle inverse est donné aux côtés donnés, il est possible d'appliquer la loi des cosenos pour déterminer la mesure du côté AC (B):

b² = A² + c² - 2e_*c _* cos b

Où:

A = BC = 15 m.

C = ab = 25 m.

B = AC.

B = 50^soit.

Les données sont remplacées:

b² = (15)² + (25)² - 2_*(quinze)_*(25) _* COS 50

b² = (225) + (625) - (750) _* 0,6427

b² = (225) + (625) - (482 025)

b² = 367 985

B = √367 985

B = 19,18 m.

Comme vous avez déjà la valeur des trois côtés, le périmètre de ce triangle est calculé:

P = côté à + côté b + côté c

P = 15 m + 25 m + 19, 18 m

P = 59,18 m

Il est désormais possible de déterminer la zone en appliquant la formule Herón, mais d'abord le semi-périmètre doit être calculé:

Sp = P ÷ 2

sp = 59,18 m ÷ 2

sp = 29,59 m.

Les mesures des côtés et du semi-périmètre dans la formule Herón sont remplacées:

Enfin, en connaissant la zone, la hauteur relative peut être calculée sur le côté C. De la formule générale, en le nettoyant, vous devez:

Zone = (côté _* H) ÷ 2

143,63 m² = (25 m _* H) ÷ 2

H = (2 _* 143,63 m²) ÷ 25 m

H = 287,3 m² ÷ 25 m

H = 11,5 m.

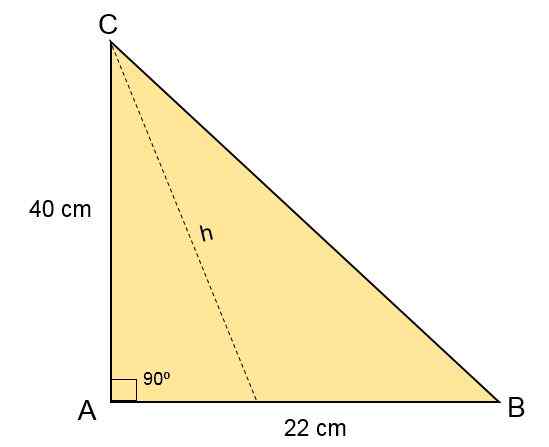
Troisième exercice

Dans le triangle Escaleno ABC, le côté B mesure 40 cm, le côté C mesure 22 cm, et dans le sommet A est un angle de 90^soit. Calculez la zone de ce triangle.

Solution

Dans ce cas, les mesures de deux côtés du triangle à l'échelle ABC sont données, ainsi que l'angle formé dans le sommet pour.

Pour déterminer la zone, il n'est pas nécessaire de calculer la mesure du côté A, car à travers des raisons trigonométriques, l'angle est utilisé pour le trouver.

Comme l'angle inverse est connu de la hauteur, cela sera déterminé par le produit d'un côté et le sein de l'angle.

Remplacement dans la formule de la zone que vous devez:

• Zone = (côté _* H) ÷ 2
• H = c _* péché a

Zone = (b _* c _* péché a) ÷ 2

Zone = (40 cm _* 22 cm _* Sen 90) ÷ 2

Zone = (40 cm _* 22 cm _* 1) ÷ 2

Zone = 880 cm² ÷ 2

Zone = 440 cm².

Les références

1. Álvaro Rendón, à. R. (2004). Dessin technique: cahier d'activité.
2. Ángel Ruiz, h. B. (2006). Géométries. CR technologique, .
3. Angel, un. R. (2007). Algèbre élémentaire. Pearson Education,.
4. Baldor, un. (1941). Algèbre. Havane: culture.
5. Barbosa, J. L. (2006). Géométrie euclidienne plate. Rio de Janeiro,.
6. Coxet, H. (1971). Fondamentaux de la géométrie. Mexique: limusa-wiley.
7. Daniel C. Alexander, G. M. (2014). Géométrie élémentaire pour les étudiants. Cengage Learning.
8. Harpe, p. d. (2000). Sujets de la théorie des groupes géométriques. University of Chicago Press.