Page d'accueil
Matematiques
Propriétés, relations et formules de trapèze rectangle, exemples

Matematiques

Propriétés, relations et formules de trapèze rectangle, exemples

UN rectangle trapèze C'est une figure plate de quatre côtés, de sorte que deux d'entre eux sont parallèles les uns aux autres, appelés bases Et aussi l'un des autres côtés est perpendiculaire aux bases.

Pour cette raison, deux des angles internes sont droits, c'est-à-dire qu'ils mesurent 90º. D'où le nom de "rectangle" qui est donné à la figure. L'image suivante d'un trapèze rectangulaire clarifie ces caractéristiques:

[TOC]

Éléments de trapèze

Les éléments du trapèze sont:

-Bases

-Sommets

-Hauteur

-Angles internes

-Base moyenne

-Diagonales

Nous détaillerons ces éléments à l'aide des figures 1 et 2:

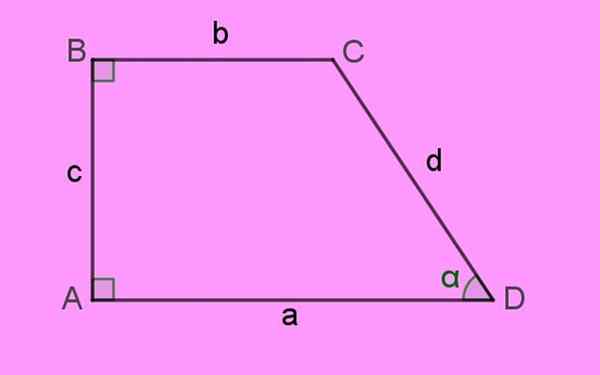
Figure 1. Un trapèze rectangle, caractérisé par deux angles internes de 90º: A et B. Source: F. Zapata.

Les côtés du trapèze rectangle sont indiqués par les lettres minuscules A, B, C et D. Les coins de la figure ou Sommets Ils sont indiqués en majuscules. Enfin Angles internes Ils sont exprimés avec des lettres grecques.

Selon la définition, le bases De ce trapèze sont les côtés A et B, qui comme observés sont parallèles et ont également une longueur différente.

Le côté perpendiculaire aux deux bases est le côté c à gauche, qui est le hauteur H du trapèze. Et enfin il y a le côté d, qui forme l'angle aigu α avec le côté a.

La somme de Angles internes d'un quadrilatère est à 360 °. Il est facilement apprécié que l'angle manquant C sur la figure est 180 - α.

La base moyenne C'est le segment qui rejoint les tas de côtés non parallèles (segment EF de la figure 2).

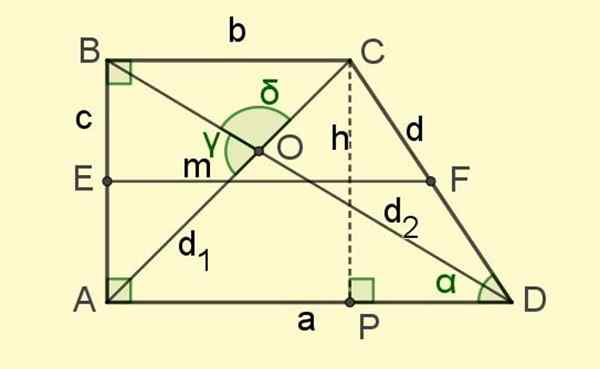Figure 2. Les éléments du trapèze rectangle. Source: F. Zapata.

Et enfin il y a les diagonales D₁ et d₂, Les segments qui unissent les sommets opposés et qui se croisent au point O (voir figure 2).

Relations et formules

Hauteur h du trapézoïde

H = c

Périmètre p

C'est la mesure du contour et est calculé en ajoutant les côtés:

Périmètre = a + b + c + d

Le côté d Il est exprimé en termes de hauteur ou de côté c À travers le théorème de Pythagore:

D = √ (a-b)² + c²

Remplacement dans le périmètre:

P = a + b + c + √ (a-b)² + c²

Base moyenne

Ce sont les semi-bornes des bases:

Base moyenne = (a + b) / 2

Parfois, la base moyenne exprimée de cette manière est trouvée:

Base moyenne = (base majeure + base mineure) / 2

Zone

La zone A du trapèze est le produit de la base moyenne par hauteur:

A = (Base majeure + base mineure) x hauteur / 2

A = (a + b) c / 2

Diagonales, côtés et angles

Plusieurs triangles apparaissent sur la figure 2, les rectangles et les non-rectangles. À ceux qui sont des triangles raisonts, ils peuvent être appliqués par le théorème de Pythagore et ceux qui ne le font pas, les théorèmes du cosinus et du sein.

Peut vous servir: Nombres transcendants: quelles sont les formules, les exemples, les exercices

De cette façon, il existe des relations entre les côtés et entre les côtés et les angles internes du trapèze.

Triangle CPA

Il est rectangle, ses jambes sont les mêmes et elles valent b, tandis que l'hypoténuse est la diagonale D₁, donc:

d₁² = b² + b² = 2B²

Triangle de tampon

C'est aussi rectangle, les jambes sont pour et c (ou aussi pour et H) Et l'hypoténuse est d₂, de manière que:

d₂² = A² + c²= A² + H²

Triangle CDA

Comme ce triangle n'est pas rectangulaire, le théorème de cosinus est appliqué, ou aussi le sein.

Selon le théorème de Coseno:

d₁² = A² + d² - 2ad cos α

Triangle CDP

Ce triangle est rectangulaire et avec ses côtés les raisons trigonométriques de l'angle α sont construites:

sin α = h / d

cos α = pd / d

Mais le côté pd = a - b, donc:

cos α = (a -b) / d → a - b = d cos α

a = b + d cos α

Vous avez aussi:

Tg α = sin α / cos α = h / (a-b) → h = tg α (a-b)

Triangle CDB

Dans ce triangle, nous avons l'angle dont le sommet est en c. Il n'est pas marqué sur la figure, mais au début, il a marqué qu'il vaut 180 - α. Ce triangle n'est pas un rectangle, donc le théorème ou le théorème du sein en cosinus peut être appliqué.

Maintenant, il peut être facilement démontré que:

Sen (180 - α) = sin α

cos (180 - α) = - cos α

Appliquer le théorème de Coseno:

d₂² = D² + b²- 2db cos (180 - α) = D² + b²+ 2db cos α

Exemples de rectangles

Les trapèzos et en particulier les rectangles se trouvent de nombreux côtés, et parfois pas toujours tangibles. Ici, nous avons plusieurs exemples:

Trapecio comme élément de conception

Les figures géométriques abondent dans l'architecture de nombreux bâtiments, comme cette église de New York, qui montre une structure sous la forme de trapèzes rectangle.

La forme trapézoïdale est également fréquente dans la conception de conteneurs, de conteneurs, de lames (Coupeur ou exact), des feuilles et en conception graphique.

figure 3. Angel à l'intérieur d'un trapèze rectangle dans une église à New York. Source: David Goehring à travers Flickr.

Générateur d'ondes trapézoïdal

Les signaux électriques peuvent non seulement être carrés, sinusoïdaux ou triangulaires. Il existe également des signaux trapézoïdaux qui sont utiles dans de nombreux circuits. Dans la figure 4, il existe un signal trapézoïdal composé de deux rectangles. Entre eux, ils forment un seul trapézoïde isocèle.

Peut vous servir: Diviseurs de 8: Quelles sont les explications faciles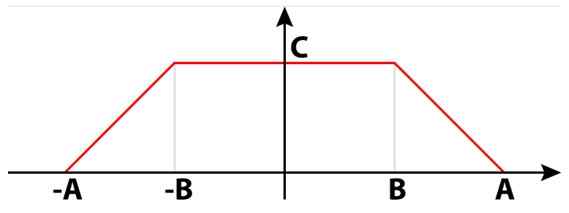

Figure 4. Un signal trapézoïdal. Source: Wikimedia Commons.

Dans le calcul numérique

Pour calculer numériquement l'intégrale définie de la fonction f (x) entre A et B, la règle de trapèze est utilisée pour approximer la zone sous le graphique de F (x). Dans la figure suivante, à gauche, les approches intégrales avec un seul rectangle trapézoïde.

Une meilleure approche est celle de la bonne figure, avec plusieurs rectangles.

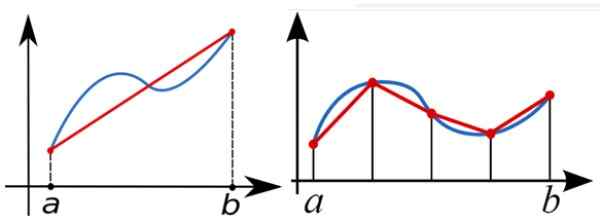Figure 5. Une intégrale définie entre A et B n'est rien d'autre que la zone sous courbe f (x) entre ces valeurs. Un trapèze rectangle peut servir de première approche de cette zone, mais plus les trapézoïdes sont utilisés, meilleur est l'approche. Source: Wikimedia Commons.

Poutre de charge trapézoïdale

Les forces ne sont pas toujours concentrées sur un seul point, car les corps sur lesquels elles agissent ont des dimensions appréciables. Tel est le cas d'un pont à travers lequel les véhicules circulent en continu, l'eau d'une piscine sur les murs verticaux du même ou un toit sur lequel l'eau ou la neige s'accumule.

C'est pourquoi les forces sont distribuées par unité de longueur, de surface ou de volume, selon le corps dont ils agissent.

Dans le cas d'un faisceau, une force distribuée par unité de longueur peut avoir diverses distributions, par exemple celle du trapèze rectangulaire illustré ci-dessous:

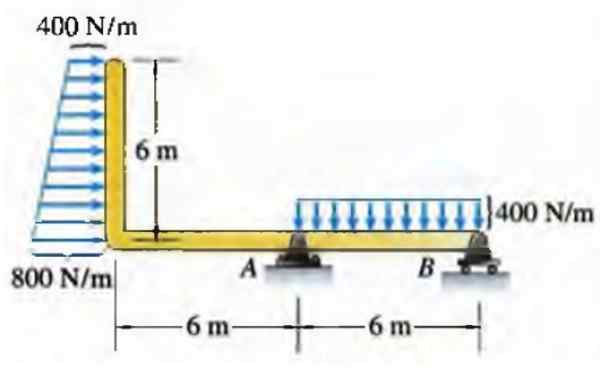Figure 6. Charges sur une poutre. Source: Bedford, à. mille neuf cent quatre vingt seize. Statique. Addison Wesley Inter -American.

En réalité, les distributions ne correspondent pas toujours à des formes géométriques régulières comme celle-ci, mais elles peuvent être une bonne approche dans de nombreux cas.

En tant qu'outil éducatif et d'apprentissage

Les blocs et les feuilles avec des formes géométriques, y compris les trapézoïdes, sont très utiles pour que les enfants se familiarisent dès leur plus jeune âge avec le monde fascinant de la géométrie.

Figure 7. Blocs avec des formes géométriques simples. Combien de rectangles sont cachés dans les blocs? Source: Wikimedia Commons.

Exercices résolus

- Exercice 1

Dans le trapèze rectangle de la figure 1, la base la plus grande vaut 50 cm et la plus petite base est égale à 30 cm, il est également connu que le côté oblique mesure 35 cm. Trouver:

A) Angle α

b) hauteur

c) périmètre

d) base moyenne

e) zone

f) Diagonale

Solution à

Les données de l'énoncé sont résumées de cette manière:

A = base supérieure = 50 cm

B = base mineure = 30 cm

D = côté incliné = 35 cm

Peut vous servir: opérations de base

Pour trouver l'angle α, nous visitons la section des formules et des équations, pour voir lequel qui convient le mieux aux données offertes. L'angle recherché se trouve dans plusieurs des triangles analysés, par exemple le CDP.

Là, nous avons cette formule, qui contient l'inconnu et aussi les données que nous connaissons:

cos α = (a-b) / d

Donc:

α = arches [(a-b) / d] = arches [(50-30) / 35] = arches 20/35 = 55.15 º

Solution B

De l'équation:

sin α = h / d

H = D.Sin α = 35 sen 55.15 º cm = 28.72 cm

Solution C

Le périmètre est la somme des côtés, et comme la hauteur est égale au côté C, nous devons:

C = h = 28.72 cm

Donc:

P = (50 + 30 + 35 + 28.72) CM = 143.72 cm

Solution d

La base moyenne est les semi-bornes des bases:

Base moyenne = (50 + 30 cm) / 2 = 40 cm

Solution E

La zone trapézoïde est:

A = base moyenne x hauteur = 40 cm x 28.72 = 1148.8 cm².

Solution F

Pour la diagonale D₁ Cette formule peut être utilisée:

d₁² = b² + b² = 2B²

d₁²= 2 x (30 cm)² = 1800 cm²

d₁ = √1800 cm² = 42.42 cm

Et pour la diagonale d₂:

d₂² = D² + b²+ 2db cos α = (35 cm)² + (30 cm)² + 2 x 35 x 30 cm² COS 55.15 º = 3325 cm²

d₂ = √ 3325 cm² = 57.66 cm

Ce n'est pas le seul moyen de trouver D₂, Puisqu'il y a aussi le triangle de tampon.

- Exercice 2

Le graphique de vitesse suivant en fonction d'un mobile qui a un mouvement rectiligne uniformément accéléré. Calculez la distance parcourue par le mobile pendant l'intervalle de temps entre 0.5 et 1.2 secondes.

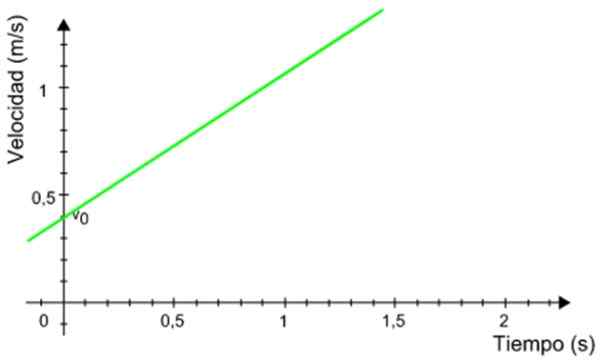Figure 8. Graphique contre le temps d'un mobile avec un mouvement de réactionnement uniforme accéléré. Source: Wikimedia Commons.

Solution

La distance parcourue par le mobile est équivalente à la zone sous le graphique, délimité par l'intervalle de temps indiqué.

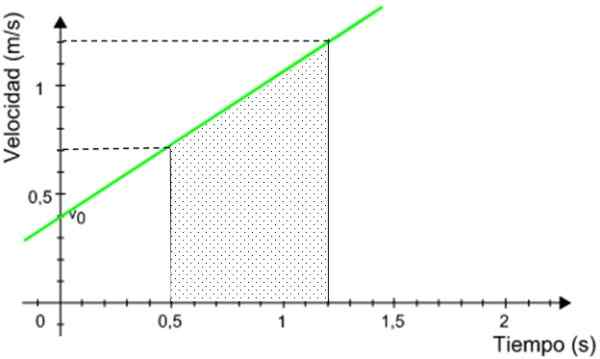Figure 9. La distance parcourue par le mobile est équivalente à la zone sous les graphiques. Source: modifiée par f. Zapata.

La zone ombrée est la zone d'un trapèzoïde rectangulaire, donné par: