Théorème de Torricelli

Qu'est-ce que le théorème de Torricelli?

Il Théorème de Torricelli o Le principe de Torricelli indique que la vitesse du liquide qui sort par le trou dans la paroi d'un réservoir ou d'un conteneur Le trou.

Le théorème est illustré dans la figure suivante:

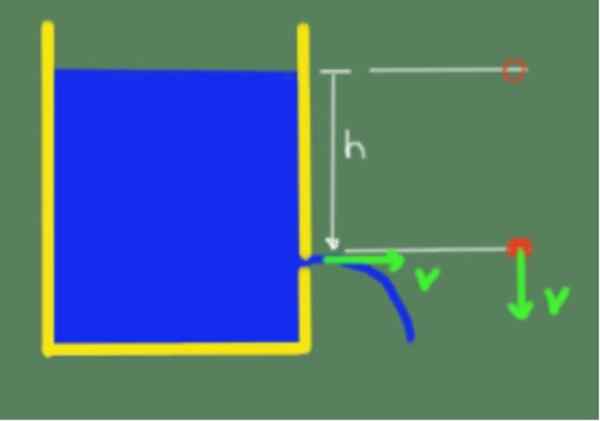Illustration du théorème de Torricelli. Source: auto-faite.

En raison du théorème de Torricelli, nous pouvons alors dire que la vitesse de sortie du liquide par un trou qui est jusqu'à la hauteur h sous la surface libre du liquide est donnée par la formule suivante:

Où g est l'accélération de la gravité et H est la hauteur du trou à la surface libre du liquide.

L'évangéliste Torricelli était un physique et un mathématicien né dans la ville de Faenza, en Italie, en 1608. Torricelli est attribué à l'invention du baromètre du mercure et en reconnaissance il y a une unité de pression appelée «torr», équivalente à un millimètre de mercure (mm de Hg).

Démonstration du théorème

Dans le théorème de Torricelli et dans la formule qui donne la vitesse, il suppose que les pertes dues à la viscosité sont méprisables, comme dans la chute libre, il est supposé que la friction due à l'air qui entoure l'objet qui tombe est insignifiant.

L'hypothèse précédente est raisonnable dans la plupart des cas et implique également la conservation de l'énergie mécanique.

Pour démontrer le théorème, nous trouverons en premier lieu la formule de vitesse pour un objet libéré avec une rapidité initiale nulle, de la même hauteur que la surface liquide dans le réservoir.

Peut vous servir: vagues à trois dimensions: concept, types et exemples

Le principe de conservation de l'énergie sera appliqué pour obtenir la vitesse de l'objet qui tombe juste au moment où une hauteur a chuté H égal à celui du trou à la surface libre.

Comme il n'y a pas de pertes de friction, il est valable d'appliquer le principe de la conservation de l'énergie mécanique. Supposons que l'objet qui chute ait la masse m et la hauteur h est mesurée à partir du niveau de sortie du fluide.

Objet qui tombe

Lorsque l'objet est libéré d'une hauteur égale à celle de la surface libre du liquide, son énergie n'est que le potentiel gravitationnel, car sa vitesse est nul et, par conséquent, son énergie cinétique est nulle. L'énergie potentielle EP est donnée par:

Ep = m g h

Quand il va devant le trou, sa hauteur est nulle, alors l'énergie potentielle est nulle, donc elle n'a que l'énergie cinétique EC donnée par:

EC = ½ m V²

Puisque l'énergie est préservée EP = EC de ce qui est obtenu:

½ m V² = m g h

Effacer la vitesse V La formule Torricelli est ensuite obtenue:

Liquide qui sort du trou

Ensuite, nous trouverons la vitesse de sortie du liquide à travers le trou, afin de démontrer qu'il coïncide avec celui qui vient d'être calculé pour un objet qui tombe librement.

Pour cela, nous compterons sur le principe de Bernoulli, qui n'est rien de plus que la conservation de l'énergie appliquée aux fluides.

Le principe de Bernoulli est formulé comme ceci:

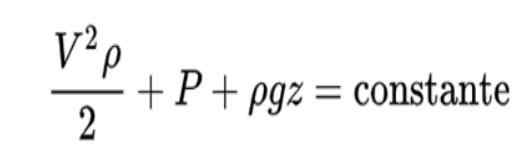
L'interprétation de cette formule est la suivante:

• Le premier terme représente l'énergie cinétique du liquide par unité de volume
• La seconde représente le travail effectué par la pression par unité de zone transversale
• Le troisième représente l'énergie potentielle gravitationnelle par unité de volume de fluide.

Peut vous servir: vitesse instantanée: définition, formule, calcul et exercices

Au fur et à mesure que nous partons de la prémisse qui est un fluide idéal, dans des conditions non turbulentes à vitesses relativement faibles, il est pertinent d'affirmer que l'énergie mécanique par volume unitaire dans le fluide est constante dans toutes les régions ou les sections transversales de la même chose.

Dans cette formule V est la vitesse du fluide, ρ Densité fluide, P la pression et z La position verticale.

Dans la figure qui apparaît ci-dessous, la formule de Torricelli est démontrée sur la base du principe de Bernoulli.

Nous appliquons la formule Bernoulli sur la surface libre du liquide que nous désignons (1) et dans le trou de sortie que nous désignons par (2). Le niveau de hauteur zéro a été choisi avec le trou de sortie.

Dans la prémisse que la section transversale en (1) est beaucoup plus grande qu'en (2), nous pouvons alors supposer que la vitesse de diminution du liquide en (1) est pratiquement négligé.

C'est pourquoi V a été placé₁= 0, la pression à laquelle le liquide est soumis en (1) est la pression atmosphérique et la hauteur mesurée du trou est H.

Pour la section de sortie (2), nous supposons que la vitesse de sortie est V, la pression à laquelle le liquide à la sortie est également soumis est la pression atmosphérique et la hauteur de sortie est nul.

Les valeurs correspondant aux sections (1) et (2) sont remplacées dans la formule de Bernoulli et égales. L'égalité est valable car nous supposons que le liquide est idéal et qu'il n'y a pas de pertes de friction visqueuses. Une fois que tous les termes ont été simplifiés, la vitesse est obtenue dans le trou de sortie.

Peut vous servir: nain rouge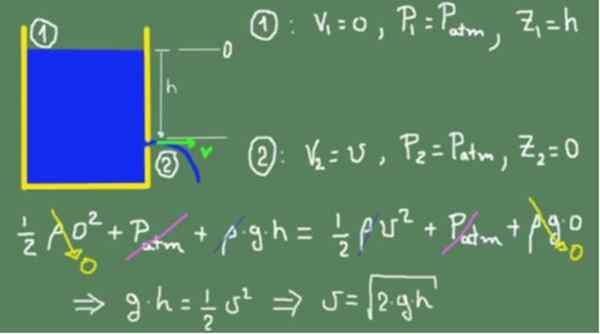

La boîte précédente montre que le résultat obtenu est le même que celui d'un objet qui tombe librement,

Avec ce qui est démontré, le principe de Torricelli.

Exercices résolus

Exercice 1

Toi) Le petit tube de sortie d'un réservoir d'eau est à 3 m sous la surface de l'eau. Calculez la vitesse de sortie de l'eau.

Solution:

La figure suivante montre comment la formule de Torricelli est appliquée à ce cas.

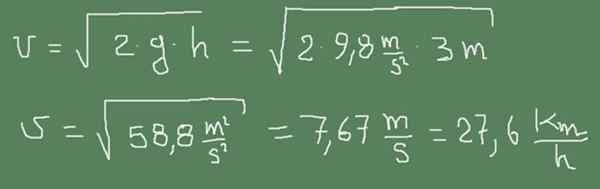
Exercice 2

Ii) En supposant que le tube de sortie du réservoir d'exercice précédent a un diamètre de 1 cm, calculez le débit de sortie d'eau.

Solution:

L'écoulement est le volume de liquide qui sort par unité de temps et est simplement calculé en multipliant la zone du trou de sortie par la vitesse de sortie.

La figure suivante montre les détails du calcul.

Exercice 3

III) Déterminez la hauteur de la surface libre de l'eau dans un récipient si connu

que dans un trou au fond du récipient, l'eau atteint 10 m / s.

Solution:

Même lorsque le trou est au bas du conteneur, la formule de Torricelli peut être appliquée.

La figure suivante montre le détail des calculs.

Les références

1. Wikipédia. Théorème de Torricelli.
2. Hewitt, P. Sciences physiques conceptuelles. CINQUIÈME ÉDITION.119.
3. Jeune, Hugh. 2016. La physique universitaire de Sears-Zansky avec la physique moderne. 14e ed. Pearson. 384.