Miletus tel théorème

Nous expliquons le premier et le deuxième théorème de tels, avec des exemples et des exercices résolus

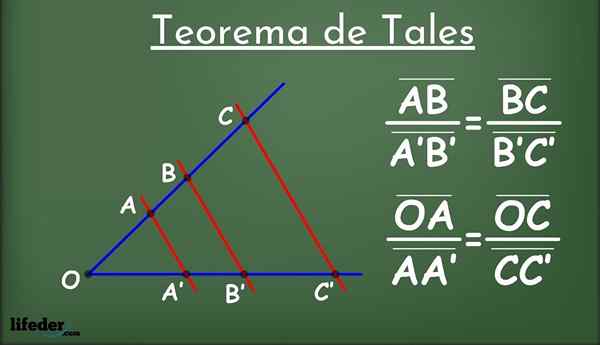
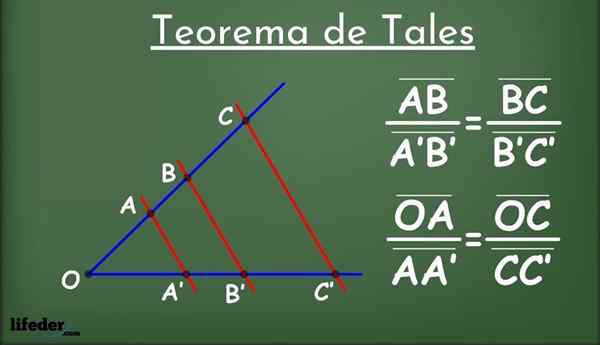Figure 1.- Le théorème des contes

Qu'est-ce que tel?

Il un tel théorème De miletus, il se réfère en fait à plusieurs théorèmes de géométrie attribués aux sages de la Grèce antique Thales de Miletus, qui a vécu de 624 à 546 AC à Miletus, la Turquie actuelle.

En plus du mathématicien et du géomètre, tel était un philosophe reconnu pour sa grande netteté. On dit qu'il a réussi à mesurer la hauteur de la grande pyramide grâce à l'utilisation de l'un de ses théorèmes.

Il Premier théorème de tel Il se réfère aux segments qu'un groupe de lignes parallèles détermine en deux lignes dans le plan. Ces segments conservent un rapport de proportionnalité, comme on le verra sous peu, qui est étendu aux côtés de deux triangles, à condition que certaines conditions soient remplies.

Ce théorème est extrêmement utile dans la pratique, car il permet de déterminer la hauteur de structures très élevées ou difficiles à accéder, sans avoir besoin de les mesurer directement. C'était précisément ce que Tales a fait lorsqu'il a mesuré la hauteur de la grande pyramide.

Pour sa part, le Deuxième théorème de cela Des points de liaison qui appartiennent à une circonférence avec un triangle rectangle enregistré, dont l'hypoténuse coïncide avec son diamètre.

Premier théorème de tel

Être deux lignes dans un avion, appelé l₁ et moi₂ (en bleu sur la figure 1) et un groupe de lignes parallèles les unes aux autres (en rouge) qui se croisent L₁ et moi₂.

Les lignes parallèles divisent les lignes en segments l₁ et moi₂: Ab, a'b ', bc, b'c' et ainsi de suite. Parmi les segments rencontrés, la relation de proportionnalité suivante est établie:

Par exemple, sur cette figure, la mesure du segment «x» est calculée par le théorème de tel, car les lignes sont coupées par plusieurs parallèles qui déterminent les segments avec une longueur connue:

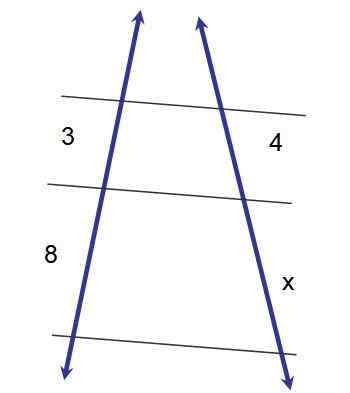Il peut vous servir: événements mutuellement exclusifs: propriétés et exemplesFigure 2.- Application du premier théorème de ce type pour déterminer la mesure du segment x. Source: F. Zapata.

3x = 32

x = 32/3 ≈ 10.7

Le théorème tel pour les triangles similaires

Le théorème peut être étendu aux triangles comme suit: Supposons qu'il y ait un triangle ABC sur lequel un segment parallèle est attiré par l'un de ses côtés. De cette façon, deux triangles similaires sont obtenus: ABC et DEC, dont les angles internes sont congruents, c'est-à-dire qu'ils ont une mesure égale.

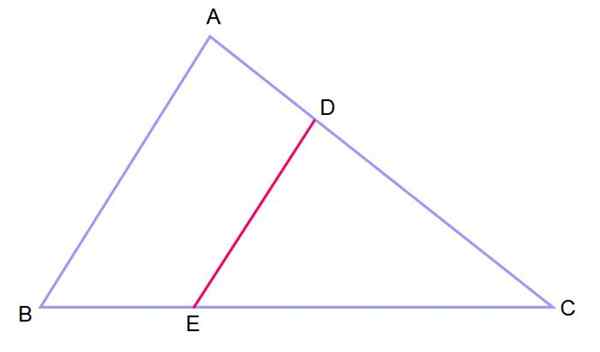figure 3.- Deux triangles en position de tel, avec deux côtés parallèles et un angle commun, sont similaires. Source: F. Zapata.

Lorsque vous avez deux triangles disposés de cette manière, il est dit qu'ils sont en position de telle position.

Un rapport de proportionnalité entre les segments est augmenté de la même manière que pour les lignes parallèles:

Qui équivaut à cet autre, entre les côtés correspondants de chaque triangle, également appelés côtés homologues:

Chacun de ces quotients est appelé Raison de similitude. Dans des triangles similaires, la raison de la similitude est égale au quotient entre les périmètres et le carré du rapport de similitude est égal au quotient entre les zones.

Ensuite, un exemple dans lequel le théorème tel peut être appliqué à des triangles similaires et à découvrir combien vaut le côté X inconnu.

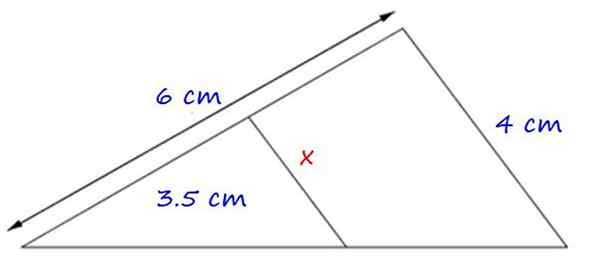Figure 4.- Exemple d'application du premier théorème de ce type. Source: F. Zapata.

Les triangles formés sont similaires, car ils ont un angle commun et les côtés x et 4 cm sont parallèles.

Par conséquent, la proportionnalité entre les côtés correspondants est:

Et la valeur de X est facilement effacée:

x = (4 × 3.5) ÷ 6 cm = 2.3 cm

Deuxième théorème de cela

Ce théorème fait référence à un triangle dont les sommets sont des points qui appartiennent à une circonférence, ce qui signifie qu'il y est enregistré.

Dans ce cas, le théorème établit que chaque fois que l'hypotenusa correspond au diamètre de la circonférence, le triangle ainsi tracé est rectangle, c'est-à-dire que l'un de ses angles internes mesure 90 °, comme le montre la figure 5 à gauche.

Peut vous servir: symbolisation des expressions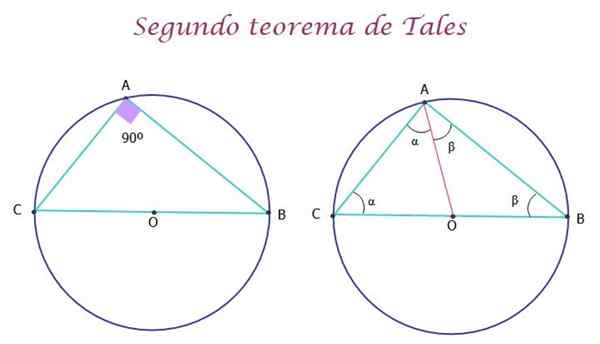Figure 5.- Le deuxième théorème de ces états que le triangle enregistré dans la circonférence est le rectangle. Source: F. Zapata.

Démonstration du deuxième théorème de tel

La démonstration du théorème est très simple. Dans la figure ci-dessus à droite, le segment AO a été dessiné en rouge, pour former les deux triangles AOC et AOB, qui sont isoscéles, car les côtés OA, OC et OB sont des radios des circonférences et donc ils mesurent les mêmes.

De cette façon, les triangles ont deux angles égaux, qui sont respectivement α et β. Maintenant, pour le triangle ABC d'origine, comme pour tout triangle, il est réalisé que la somme des mesures de ses angles internes est donc égale à 180 °:

α + (α + β) + β = 180º

Ainsi:

2α + 2β = 180º

Donc:

2 (α + β) = 180º

α + β = 90º

Ce qui prouve que le triangle ABC a un angle interne de 90 ° et est donc un triangle droit.

Exemple

Dans la figure suivante, le triangle ABC est isocèle et rectangle (triangle Isorectangle), étant le périmètre de la circonférence égale à 25 cm. Combien coûtent les segments AC et AB?

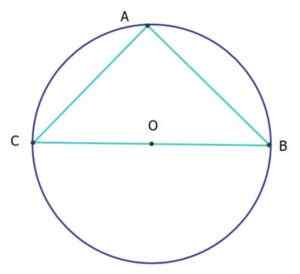
Le périmètre de la circonférence est sa longueur L, administré en fonction de son diamètre D par formule:

L = πd

Par conséquent, le diamètre, qui est le segment CB, mesure:

D = cb = l / π = 25 cm / π = 7.96 cm.

Puisque le triangle est isoscèle, cela signifie que ses angles aigus mesurent 45º chacun. Comme l'hypoténuse du triangle est le diamètre de la circonférence, un rapport trigonométrique de 45 peut être utilisé, par exemple:

Sen 45º = AC / CB

AC = CB × sin 45º = 7.96 cm × sin 45º = 5.64 cm

Peut vous servir: théorème de moivre

Le côté AB a la même mesure: 5.64 cm, puisque le triangle est isocèle.

Ces applications de théorème

Le premier théorème de ce type peut être utilisé pour connaître des distances qui ne sont pas facilement mesurables. On dit que tel s'est rendu en Égypte et qu'il a déterminé, d'une manière très ingénieuse, de la hauteur de la grande pyramide.

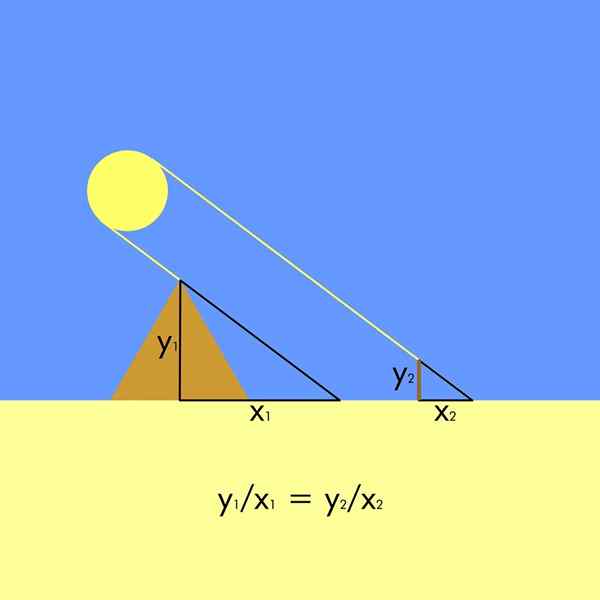
Pour cela, c'était nécessaire. Ainsi, deux triangles similaires se forment, car les rayons du soleil ont une incidence parallèle.

Dans la figure, la hauteur de la pyramide est et₁ Et son ombre est x₁, Tandis que la hauteur du pieu est et₂ (Certains chroniqueurs affirment que tels ont utilisé leur propre taille) et leur ombre est x₂. Comme les triangles sont similaires, la relation de proportionnalité suivante est formée:

Étant très facile à effacer la hauteur de la pyramide et₁:

et₁ = x₁∙ (et₂ ÷ x₂)

Les références

1. Alexander, D. 2013. Géométrie. 5e. Édition. Cengage Learning.
2. Requena, b. Un tel théorème. Récupéré de: universoformules.com.
3. Salle mathématique. Tales de mileto et la grande pyramide. Récupéré de: salonmatématique.com
4. Matériel didactique superprof. Milétus tel. Récupéré de: superprof.est.
5. Théorème de thales et de ressemblance. Deux problèmes très anciens. Récupéré de: edu.Xunta.Fille.