Formule de principe Archimède, démonstration, applications

Il Le principe d'Archimede Il dit qu'un corps totalement ou partiellement submergé reçoit une force verticale appelée pousser, ce qui équivaut au poids du volume de liquide déplacé par le corps. 

Certains objets flottent dans l'eau, d'autres coulent et certains se plongent partiellement. Pour couler un ballon de plage, il est nécessaire de faire un effort, car cette force est immédiatement perçue qui essaie de la retourner à la surface. Au lieu de cela, une sphère métallique coule rapidement. 

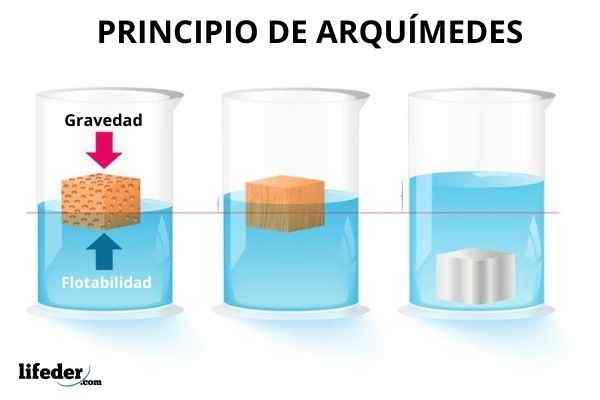
D'un autre côté, les objets submergés semblent plus légers, il y a donc une force exercée par le liquide qui s'oppose au poids. Mais vous ne pouvez pas toujours compenser du tout à la gravité. Et, bien qu'il soit plus évident avec l'eau, les gaz sont également capables de produire cette force sur les objets immergés en eux.

[TOC]

Histoire

Archimède de Syracuse (287-212 A. C.) C'est celui qui devait avoir découvert ce principe, étant l'un des plus grands scientifiques de l'histoire. Ils disent que King Hierón II de Syracuse a envoyé un orfèvre pour fabriquer une nouvelle couronne, pour laquelle il lui a remis une certaine quantité d'or.

Archimède

Lorsque le roi a reçu la nouvelle couronne, il avait le bon poids, mais il soupçonnait que l'orfèvre l'avait trompé en ajoutant de l'argent au lieu de l'or. Comment puis-je le vérifier sans détruire la couronne?

Hierón a appelé Archimède, dont la renommée du savant était bien connue, pour l'aider à résoudre le problème. La légende affirme qu'Archimède a été immergé dans la baignoire lorsqu'il a trouvé la réponse et, telle était son émotion, qu'il a couru nu dans les rues de Syracuse pour chercher le roi criant "Eureka", ce qui signifie "je l'ai trouvé".

https: // giphy.com / gifs / stito3echtlnbvliz3

Qu'est-ce qu'Archimède a trouvé? Eh bien, lorsque vous prenez une salle de bain, le niveau d'eau dans la baignoire, lorsqu'il est entré, ce qui signifie qu'un corps submergé déplace un certain volume de liquide.

Et si j'avais submergé la couronne dans l'eau, elle devait également déplacer un certain volume d'eau si la couronne était en or et une autre si elle était en alliage avec de l'argent.

Formule de principe d'Archimède

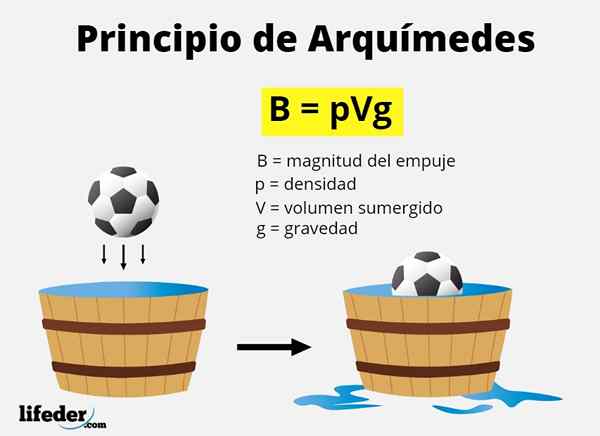
La force promotionnelle mentionnée dans le principe d'Archimède est connue sous le nom pousser hydrostatique soit force de flottaison Et, comme nous l'avons dit, il équivaut au poids du volume de fluide déplacé par le corps lorsqu'il est submergé.

Le volume déplacé est équivalent au volume de l'objet submergé, totalement ou partiellement. Puisque le poids de tout est mg, Et la masse du liquide est Densité x volume, Nier comment B à l'ampleur de la poussée, il faut mathématiquement:

B = m_courant x g = densité de fluide x Volume immergé x Gravité

B = ρ_courant X V_submergé x g

Où la lettre grecque ρ ("rho") dénote la densité.

Le poids apparent

Le poids des objets est calculé par l'expression bien connue mg, Cependant, les choses semblent plus légères lorsqu'ils sont submergés dans l'eau. 

Il poids apparent d'un objet est ce qui a quand il est immergé dans l'eau ou un autre liquide et le savoir, vous pouvez obtenir le volume d'un objet irrégulier comme la couronne du roi Hierón, comme on le verra ci-dessous.

Peut vous servir: 13 exemples de la première loi de Newton dans la vraie vie

Pour ce faire, il est complètement submergé dans l'eau et soumis à une corde attachée à un dynamomètre -un instrument fourni avec un ressort qui sert à mesurer les forces-. Plus le poids de l'objet est élevé, plus l'allongement du ressort est important, qui est mesuré sur une échelle fournie dans l'appareil.

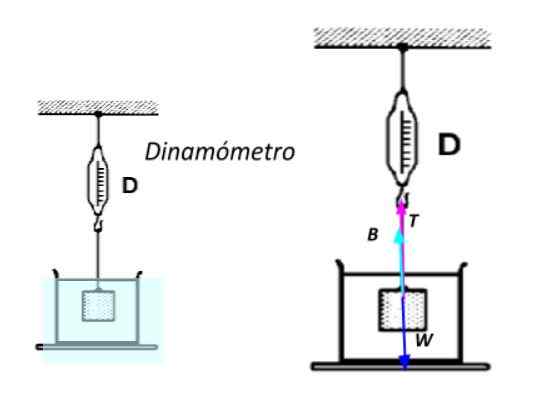Poids apparent d'un objet immergé. Source: Préparé par F. Zapata.

Appliquer la deuxième loi de Newton en sachant que l'objet est au repos:

Σf_et = B + t - w = 0

Le poids apparent w_pour Il équivaut à la tension sur la corde T:

T = w_pour

W_pour = mg - ρ_courant . V. g

Si le volume submergé V est requis, il est effacé comme:

V = (w - w_pour ) / ρ_courant  . g

Manifestation

https: // giphy.com / gifs / mcphppgtnpbhl4cgaq

Lorsqu'un corps s'immerge, la poussée est la force résultant de toutes les forces qui sont exercées sur le corps par la pression causée par le fluide environnant:

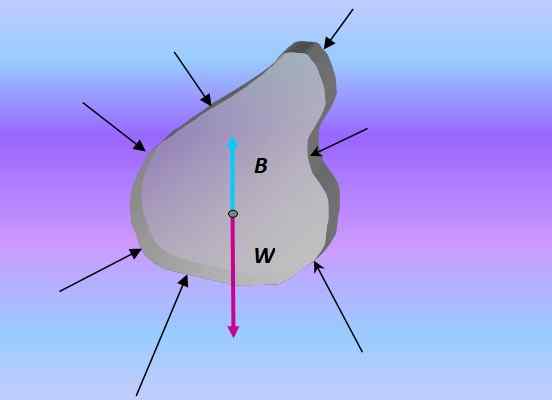Diagramme corporel libre d'un objet submergé. Source: Préparé par F. Zapata.

Pression et profondeur

Puisque la pression augmente avec la profondeur, le résultat de ces forces est toujours dirigé verticalement vers le haut. Par conséquent, le principe d'Archimède est une conséquence du théorème fondamental de l'hydrostatique, qui relie la pression P exercée par un liquide avec la profondeur z comme:

P = ρ.g.z

Forces sur un liquide d'équilibre statique

Pour démontrer le principe d'Archimède, une petite partie de repos cylindrique est prise au repos pour analyser les forces exercées dessus, comme le montre la figure suivante. Les forces sur la surface incurvée du cylindre sont annulées les unes avec les autres. 

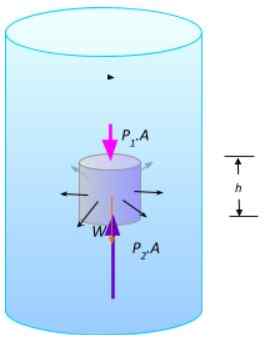Une partie du liquide en équilibre. Source: Préparé par F. Zapata.

Les amplitudes des forces verticales sont F₁ = P₁.A et F₂ = P2.A, il y a le poids W. Comme le liquide est en équilibre, la somme des forces doit être annulée:

∑F_et = P₂.A- p₁.A- w = 0

P₂.A- p₁.A = w

Étant donné que la poussée compense le poids, puisque la partie fluide est au repos, alors:

B = p₂.A- p₁.A = w

De cette expression, il s'ensuit que la poussée est due à la différence de pressions entre la face supérieure du cylindre et le plus bas. Comme W = mg = ρcourant. V. g, il faut que:

B = ρ_courant. V_submergé. g

Qui est précisément l'expression de la poussée mentionnée dans la section précédente.

Applications de principes d'Archimède

Ballons qui flottent: principe archimède en action

Le principe d'Archimède apparaît dans de nombreuses applications pratiques, parmi lesquelles nous pouvons nommer:

- Le ballon aérostatique. Qui en ayant une densité moyenne inférieure à celle de l'air environnant, flotte dedans en raison de la force de poussée.

- Les bateaûx. Le casque du navire est plus lourd que l'eau. Mais si la coque est considérée comme l'air à l'intérieur, le quotient entre la masse totale et le volume est inférieur à celui de l'eau et c'est la raison pour laquelle les navires flottent.

- Les gilets de vie. Lorsqu'ils sont construits en matériaux légers et poreux, ils sont capables de flotter parce que le rapport masse-volume est inférieur à celui de l'eau.

- Le flottant pour fermer le robinet de remplissage d'un réservoir d'eau. C'est une sphère pleine d'air de grand volume qui flotte sur l'eau, qui provoque la force de poussée - multipliée par l'effet de levier - ferme le capuchon du robinet de remplissage d'un réservoir d'eau lorsqu'il a atteint le total du niveau total.

Il peut vous servir: vagues unidimensionnelles: expression mathématique et exemples

Exemples

Exemple 1

La légende dit que le roi Hierón a donné à l'orfèvre une certaine quantité d'or pour faire une couronne, mais le monarque méfiant pensait que l'orfèvre aurait pu tricher lorsqu'il plaçait un métal moins précieux à l'intérieur de la couronne que la couronne. Mais comment pourrais-je savoir sans détruire la couronne? 

Le roi a commandé Archimède et ceci, à la recherche de la solution, a découvert son célèbre principe.

Supposons que la couronne pèse 2,10 kg-f dans l'air et 1,95 kg-f lorsqu'elle est complètement submergée dans l'eau. Dans ce cas, il n'y a pas de tromperie?

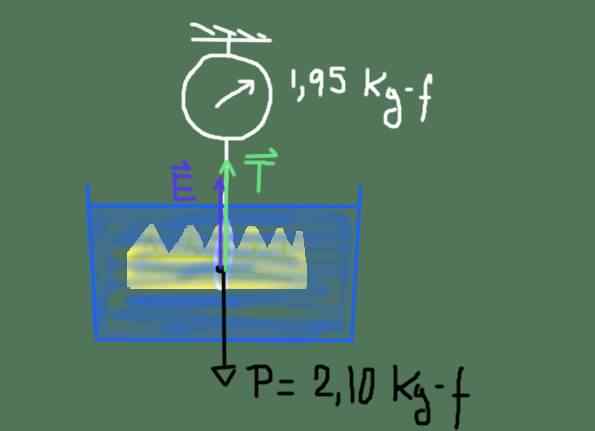Diagramme du corps libre de la couronne du roi Heron. Source: Préparé par F. Zapata

Le diagramme des forces est illustré dans la figure précédente. Ces forces sont: le poids P de la couronne, la poussée ET et la tension T de la corde qui pend à l'échelle.

P = 2,10 kg-f et t = 1,95 kg-f est connu, il est nécessaire de déterminer l'ampleur de la poussée ET:

T + e = p ⇒ e = p - t = (2,10 - 1,95) kg -f = 0,15 kg -f

En revanche, selon le principe d'Archimède, la poussée équivaut au poids de l'eau expulsée de l'espace occupé par la couronne, c'est-à-dire la densité de l'eau par le volume de la couronne en raison de l'accélération de la gravité :

E = ρ_eau⋅v⋅g = 1000 kg / m ^ 3 ⋅ V ⋅ 9,8m / s ^ 2 = 0,15 kg ⋅ 9,8 m / s ^ 2

Où le volume de la couronne peut être calculé:

V = 0,15 kg / 1000 kg / m ^ 3 = 0,00015 m ^ 3

La densité de la couronne est le quotient entre la masse de la couronne hors de l'eau et le volume de celui-ci:

Densité de la couronne = 2,10 kg / 0,00015 m ^ 3 = 14000 kg / m ^ 3

La densité de l'or pur peut être déterminée par une procédure similaire et le résultat est 19300 kg / m ^ 3.

En comparant les deux densités, il est évident que la couronne n'est pas de l'or pur! 

Exemple 2 

Sur la base des données et du résultat de l'exemple 1, il est possible de déterminer la quantité d'or volée par l'orfèvre dans le cas où une partie de l'or a été remplacée par l'argent, qui a une densité de 10500 kg / m ^ 3 3 3.

Nous appellerons ρc à la densité de la couronne, ρo à la densité d'or et ρ_p à la densité de l'argent.

La masse totale de la couronne est:

M = ρc⋅v = ρo⋅vo + ρ_p⋅vp

Le volume total de la couronne est le volume d'argent plus le volume d'or:

V = vo + vp ⇒ vp = v - vo

Remplacement dans l'équation de masse:

ρc⋅v = ρo⋅vo + ρ_p⋅ (v - vo) ⇒ (ρo - ρ_p) Vo = (ρc - ρ_p) V

C'est-à-dire que le volume d'or qui contient la couronne du volume total V est:

Vo = v⋅ (ρc - ρ_p) / (ρo - ρ_p) =…

… = 0,00015 m ^ 3 (14000 - 10500) / (19300 - 10500) = 0,0000596 m ^ 3

Pour connaître le poids en or qui contient la couronne, nous multiplions VO pour la densité de l'or:

Peut vous servir: règle de droite

MO = 19300 * 0,00005966 = 1 1514 kg

Comme la masse de la couronne est de 2,10 kg, nous savons que 0,94858 kg d'or ont été volés par l'orfèvre et remplacés par l'argent.

Exercices résolus

Exercice 1

Un énorme ballon d'hélium est capable de se soutenir en équilibre (sans monter ou descendre) à une personne.

Supposons que le poids de la personne, plus le panier, les cordes et le ballon est de 70 kg. Quel est le volume d'hélium nécessaire pour que cela se produise? Quelle taille le ballon aura-t-il?

Solution

Nous supposerons que la poussée est produite principalement par le volume d'hélium et que la poussée du reste des composants est très petite par rapport à celle de l'hélium qui occupe beaucoup plus de volume.

Dans ce cas, un volume d'hélium sera nécessaire de fournir une poussée de poids de 70 kg +.

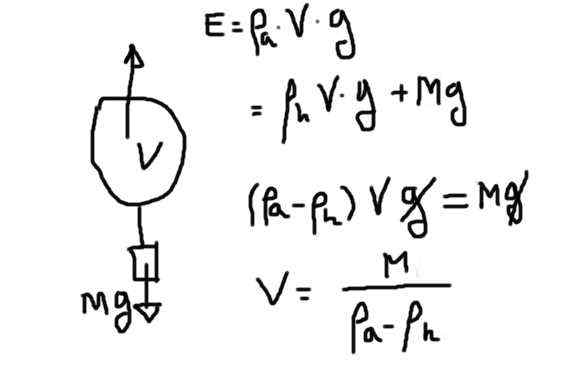Corps libre fdiaogramme plein d'hélium. Source: Préparé par F. Zapata.

La poussée est le produit du volume d'hélium en raison de la densité de l'hélium en raison de l'accélération de la gravité. Cette poussée doit compenser le poids de l'hélium plus le poids du reste.

Da⋅v⋅g = da⋅v⋅g + m⋅g

où il conclut que v = m / (da - dh)

V = 70 kg / (1.25 - 0,18) kg / m ^ 3 = 65.4 m ^ 3

C'est-à-dire que 65 sont nécessaires.4 m ^ 3 d'hélium à la pression atmosphérique pour le soutien.

Si nous supposons un ballon sphérique, nous pouvons trouver le rayon de la même chose de la relation entre le volume et le rayon d'une sphère:

V = (4/3) ⋅π⋅r ^ 3

Où r = 2,49 m. En d'autres termes, un diamètre de 5 m plein d'hélium sera nécessaire.

Exercice 2

Matériaux de densité plus faible que l'eau flottent dans le même. Supposons que vous avez des cubes de polystyrène (bouchon blanc), du bois et de la glace. Ses densités en kg par mètre cube sont respectivement: 20, 450 et 915.

Trouvez quelle fraction du volume total est hors de l'eau et quelle hauteur se démarque par rapport à la surface de l'eau en tant que densité des derniers 1000 kilogrammes par mètre cube.

Solution 

La flottabilité se produit lorsque le poids corporel est égal à la poussée due à l'eau:

E = m⋅g

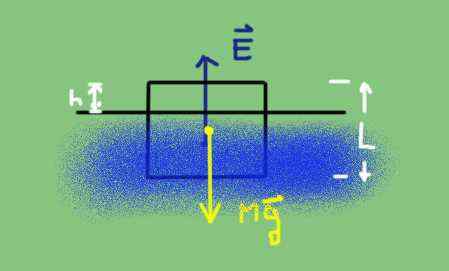Diagramme corporel libre d'un objet partiellement submergé. Source: Préparé par F. Zapata.

Le poids est la densité corporelle DC multipliée par son volume V et par l'accélération de la gravité G.

La poussée est le poids du fluide déplacé selon le principe d'Archimède et est calculé en multipliant la densité D de l'eau par le volume submergé V 'et par l'accélération de la gravité.

C'est-à-dire:

D⋅v'⋅g = dc⋅v⋅g

Ce qui signifie que la fraction de volume submergé est égale au quotient entre la densité corporelle et la densité de l'eau.

(V '/ v) = (dc / d) 

C'est-à-dire que la fraction de volume exceptionnelle (v "/ v) est

(V "/ v) = 1 - (dc / d)

Ouais H C'est la hauteur exceptionnelle et L Le côté cube La fraction de volume peut être écrite comme

(H⋅l ^ 2) / (l ^ 3) = h / l, En d'autres termes, la fraction de hauteur exceptionnelle est également

(h / l) = 1 - (dc / d)

Ensuite, les résultats des matériaux demandés sont:

Polystyrène (liège blanc):

(H / l) = (v "/ v) = 1 - (dc / d) = 1- (20/1000) = 98% hors de l'eau

Bois:

(h / l) = (v "/ v) = 1 - (dc / d) = 1- (450/1000) = 55% hors de l'eau

Glace:

(h / l) = (v "/ v) = 1 - (dc / d) = 1- (915/1000) = 8.5% hors de l'eau

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill. 417-455.
2. Cengel Y, Cimbala J. 2011.Mécanique des fluides. Fondamentaux et applications. Première édition. McGraw Hill.
3. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 4. Fluides et thermodynamique. Édité par Douglas Figueroa (USB). 1 - 42.
4. Giles, R. 2010. Mécanique fluide et hydraulique. McGraw Hill. 
5. Rex, un. 2011. Fondamentaux de la physique. Pearson. 239-263.
6. Tippens, P. 2011. Physique: concepts et applications. 7e édition. McGraw Hill.