Périmètre du cercle comment le sortir et les formules, les exercices résolus

Il périmètre du cercle C'est l'ensemble de points qui forment le contour d'un cercle et est également connu longueur de la circonférence. Cela dépend du rayon, car une circonférence plus grande aura évidemment un plus grand contour.

Être P Le périmètre d'un cercle et R le rayon de même, alors nous pouvons calculer P Avec l'équation suivante:

P = 2π.R

Le périmètre du cercle (dans ce cas une pizza) dépend de sa radio. Source: Pixabay.

Où π est un nombre réel (lit "pi") qui vaut environ 3.1416… les points suspendus sont dus au fait que π a des décimales infinies. Par conséquent, lorsque vous effectuez les calculs, il est nécessaire de contourner sa valeur.

Cependant, pour la plupart des applications, il suffit de prendre le montant indiqué ici, ou d'utiliser toutes les décimales que la calculatrice avec laquelle il fonctionne.

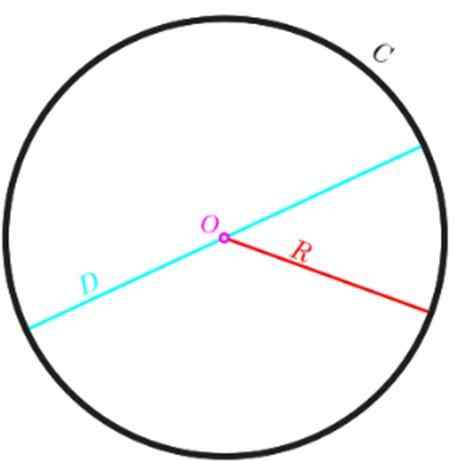
Si au lieu d'avoir le rayon, il est préféré utiliser le diamètre D, ce que nous savons est le deux fois le rayon, le périmètre est exprimé comme suit:

P = π.2r = π.D

Comme le périmètre est une longueur, il doit toujours être exprimé en unités telles que les mètres, les centimètres, les pieds, les pouces et plus encore, selon le système préféré.

[TOC]

Circonférences et cercles

Ce sont souvent des termes utilisés de manière interchangeable, c'est-à-dire que les synonymes. Mais il arrive qu'il y ait des différences entre elles.

Le mot "périmètre" vient de la "période" grecque qui signifie contour et "métro" ou mesure. La circonférence est le contour ou le périmètre du cercle. En forme, il est défini:

Une circonférence est l'ensemble de points à distance égale à un point appelé centre, cette distance étant le rayon de la circonférence.

Pour sa part, le cercle est défini comme suit:

Un cercle est l'ensemble de points dont la distance à un point appelé centre est inférieure ou égale à une distance fixe appelée radio.

Le lecteur peut avertir la différence subtile entre les deux concepts. La circonférence ne fait référence à l'ensemble des points de bord, tandis que le cercle est l'ensemble des points du bord à l'intérieur, dont la circonférence est la bordure.

Peut vous servir: exercices de dégagement de la formule

Exercices dÉmostration du calcul du périmètre du cercle

Grâce aux exercices suivants, les concepts décrits seront mis en pratique, ainsi que d'autres qui seront expliqués à leur apparaître. Nous allons partir du plus simple et le degré de difficulté sera progressivement augmenté.

- Exercice 1

Trouvez le périmètre et la zone du cercle radio de 5 cm.

Solution

L'équation donnée au début est appliquée directement:

P = 2π.R= 2π.5 cm = 10 π cm = 31.416 cm

Pour calculer la zone POUR La formule suivante est utilisée:

POUR = π.R² = π. (5cm)²= 25π cm²= 78.534 cm²

- Exercice 2

a) Trouvez le périmètre et la zone de la région vide de la figure suivante. Le centre du cercle ombré est au point rouge, tandis que le centre de la circonférence blanche est le point vert.

b) Répétez la section précédente pour la région ombrée.

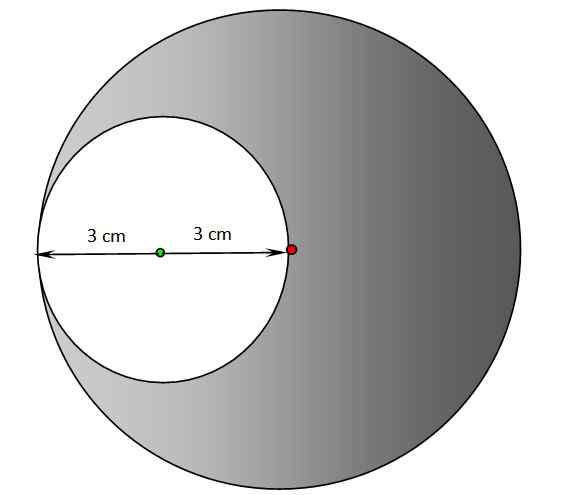Cercles pour l'exercice 2. Source: F. Zapata.

Solution

a) Le rayon de la circonférence blanche est de 3 cm, donc nous appliquons les mêmes équations que dans l'exercice 1:

P = 2π.R= 2π.3 cm = 6 π cm = 18.85 cm

POUR = π.R² = π. (3cm)²= 9π cm²= 28.27 cm²

b) Pour le cercle ombré, le rayon est de 6 cm, son périmètre est le double de celui calculé dans la section A):

P = 2π.R= 2π.6 cm = 12 π cm = 37.70 cm

Et enfin la zone de la région ombrée est calculée comme suit:

- Le premier est la zone du cercle ombragé comme s'il était complet, que nous appellerons ', comme ceci:

POUR' = π.R²= π.(6 cm)² = 36π cm²= 113.10 cm²

- Puis dans la région POUR' La zone du cercle blanc est soustraite, précédemment calculée dans la section A), de cette manière la zone demandée est obtenue, qui sera indiquée simplement comme suit:

A = a '- 28.27 cm² = 113.10-28.27 cm² = 84.83 cm²

- Exercice 3

Trouvez la zone et le périmètre de la région ombragée dans la figure suivante:

Peut vous servir: angles supplémentaires: quels sont les calculs, les exemples, les exercices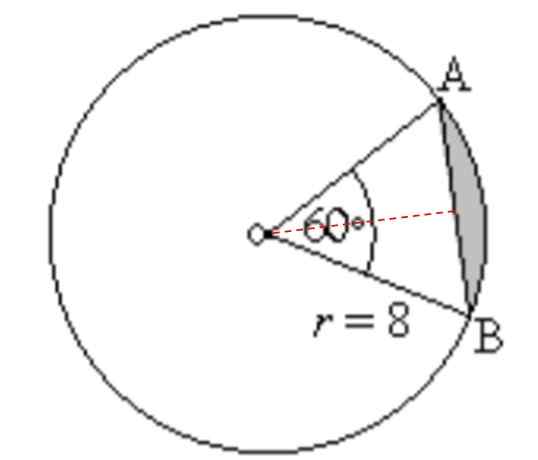Figure pour l'exercice 3. Source: F. Zapata.

Solution

Calcul de la zone de la région ombrée

Nous calculons d'abord la zone de la Secteur circulaire ou coin, entre les segments droits OA et OB et le segment Circulaire AB, comme indiqué sur la figure suivante:

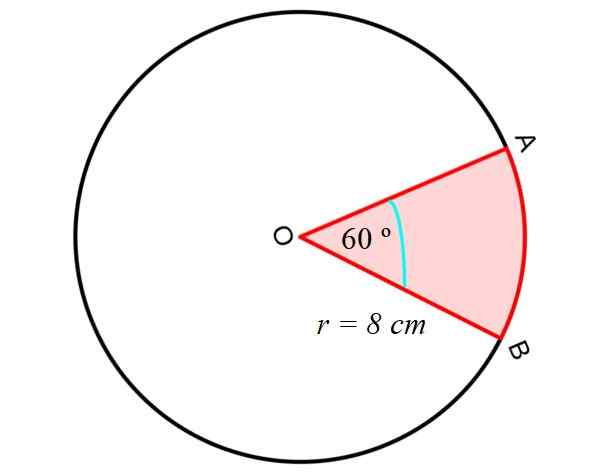
Pour cela, l'équation suivante est utilisée, ce qui nous donne la zone d'un secteur circulaire, connaissant le rayon R et l'angle central entre les segments OA et OB, c'est-à-dire deux des radios de la circonférence:

POUR _{Secteur circulaire} = Π.R². (αº / 360º)

Où αº est l'angle central - il est central car son sommet est le centre de la circonférence - entre deux radios.

Étape 1: Calcul de la zone du secteur circulaire

De cette façon, la zone du secteur représenté sur la figure est:

POUR _{Secteur circulaire} = Π.R². (αº / 360º) = π. (8 cm)². (60º / 360º) = (64/6) π cm²= 33.51 cm²

Étape 2: Calcul de la zone du triangle

Ensuite, nous calculerons la zone du triangle blanc de la figure 3. Ce triangle est équilatéral et sa zone est:

POUR _Triangle = (1/2) Base x hauteur

La hauteur est la ligne rouge en pointillé vue sur la figure 4. Pour le trouver, vous pouvez utiliser le théorème de Pythagore, par exemple. Mais ce n'est pas le seul moyen.

Le lecteur d'observateur aura remarqué que le triangle équilatéral est divisé en deux rectangles identiques, dont la base est de 4 cm:

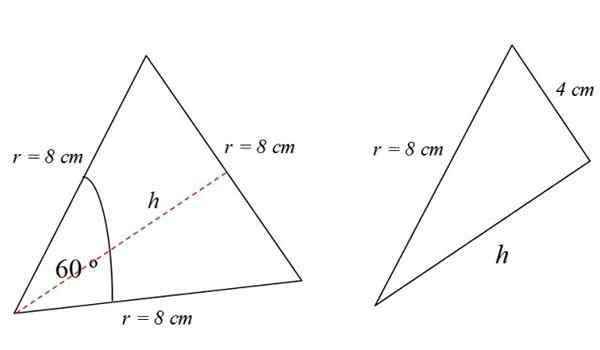
Dans un triangle droit, le théorème de Pythagore est donc accompli:

Puisque vous avez la hauteur du triangle, à la fois du rectangle et de l'équilatéral, sa zone est calculée:

POUR _Triangle = (1/2) base x hauteur = (1/2) 8 cm x 6.93 cm = 27.71 cm².

Étape 3: Calcul de la zone ombrée

Il suffit de soustraire la zone principale (celle du secteur circulaire) de la zone mineure (celle du triangle équilatéral): a _{région ombrée} = 33.51 cm² - 27.71 cm² = 5.80 cm².

Calcul du périmètre de la région ombragée

Le périmètre fouillé est la somme du côté rectiligne de 8 cm et de l'arc de circonférence AB.  Cependant, la circonférence complète sous-tend 360 º, donc un arc qui sous-the 60 º est une sixième partie de toute la longueur, que nous savons est 2.π.UN:

Peut vous servir: fonction de croissance: comment l'identifier, des exemples, des exercices

Ab = 2.π.R / 6 = 2.π.8 cm / 6 = 8.38 cm

Remplacement, le périmètre de la région ombragée est:

P = 8 cm + 8.38 cm = 16.38 cm.

Applications

Le périmètre, comme la région, est un concept très important en géométrie et avec de nombreuses applications dans la vie quotidienne.

Les artistes, les concepteurs, les architectes, les ingénieurs et de nombreuses autres personnes utilisent le périmètre tout en développant leur travail, en particulier celui d'un cercle, car la forme ronde est partout: de la publicité, à travers la nourriture aux machines.

La circonférence et le cercle sont parmi les géométries les plus utilisées. Source: Pixabay.

Pour connaître directement la longueur d'un cercle, il suffit de l'envelopper avec un fil ou une chaîne, puis étendre ce fil et le mesurer avec un ruban adhésif. L'autre alternative est de mesurer le rayon ou le diamètre du cercle et d'utiliser certaines des formules décrites ci-dessus.

Dans le travail quotidien, le concept de périmètre est utilisé lorsque:

-Le moule approprié est choisi pour une certaine pizza ou la taille du gâteau.

-Une route urbaine sera conçue, en calculant la taille d'un rougeome où les voitures peuvent se tourner pour changer de sens.

-Nous savons que la terre tourne autour du soleil sur une orbite approximativement circulaire - en réalité que les orbites planétaires sont elliptiques, selon les lois de Kepler - mais la circonférence est une très bonne approche de la plupart des planètes.

-La taille appropriée d'un anneau ou d'une bague qui sera achetée dans une boutique en ligne est choisie.

-Nous choisissons une clé à la bonne taille pour desserrer un écrou.

Et beaucoup plus.

https: // youtu.Be / cr8xjryl5tk

Les références

1. Tutoriels de mathématiques gratuits. Zone et périmètre d'un cercle - calculatrice de géométrie. Récupéré de: Analyzemath.com.
2. Référence ouverte en mathématiques. Circonférence, périmètre d'un cercle. Récupéré de: MathpenRef.com.
3. Institut Monterey. Périmètre et zone. Récupéré de: montereyinstitute.org.
4. Science. Comment trouver le périmètre d'un cercle. Récupéré de: science.com.
5. Wikipédia. Circonférence. Récupéré de: dans.Wikipédia.org.