Signes de la loi

Nous expliquons la loi des signes, avec des exemples et des exercices résolus

Schéma de la loi sur les signes

Quelle est la loi des signes?

La Signes de la loi C'est l'ensemble des règles utilisées dans les calculs arithmétiques et algébriques avec des nombres réels pour attribuer correctement le signe au résultat, lorsque des quantités positives et négatives sont impliquées.

Il existe des règles adéquates selon l'opération qui est effectuée: somme, soustraction, multiplication et division, qui sont les plus fondamentales, et il existe également des règles de signes liés aux opérations de potentialisation et de dépôt.

Dans une opération donnée, que ce soit à la main ou avec la calculatrice, il est nécessaire d'appliquer correctement la loi des panneaux pour garantir un résultat correct, car un petit changement dans les panneaux modifie considérablement les montants.

La loi des signes pour chaque opération arithmétique de base et les cas qui peuvent survenir sont examinés ci-dessous.

Loi des signes en somme

1) Si les chiffres à ajouter ont le même signe

Les nombres sont ajoutés comme d'habitude et le résultat est ajouté au signe des chiffres, que ce soit positif ou négatif.

Il est important de garder à l'esprit que les nombres positifs ne sont généralement pas avant le signe, mais sont écrits directement. D'un autre côté, des nombres négatifs sont écrits entre parenthèses, surtout lorsqu'ils sont précédés par le symbole d'une opération arithmétique, afin d'éviter la confusion.

Exemples de sommes de nombres avec le même signe:

3 + 9 = 12
4 + 7 + 1 + 6 = 18
(−3) + (−8) = −11
(−5) + (−10) + (−6) = −21

2) Si les nombres à ajouter ont un signe différent

Les nombres sont soustraits et le signe du nombre qui a la plus grande valeur absolue est ajouté au résultat, qu'il soit positif ou négatif.

À titre d'exemple, effectuez l'opération 5 + (−14). Comme la valeur absolue de (−14) est supérieure à la valeur absolue de 5, 5 unités sont soustraites de 14, ce qui donne 9 et ce résultat est placé le signe négatif:

Peut vous servir: prismes et pyramides

5 + (−14) = −9

Plus d'exemples de cette règle appliqués à la somme de deux nombres de signes différents sont:

(−27) + 12 = −15

12 + (−7) = 5

Si dans l'opération, il y a plus de deux ajouts avec des signes différents, le propriété associative de la somme:

(−20) + 9 + (−7) = [(−20) + 9] + (−7)

L'opération est d'abord effectuée dans Pracete, qui se compose de la somme de deux nombres de signes différents, pour lesquels la règle décrite est appliquée: le résultat est soustrait et le signe du nombre avec la valeur absolue la plus élevée:

(−20) + 9 = −11

L'opération est comme ceci:

(−20) + 9 + (−7) = (−11) + (−7)

Maintenant, vous avez la somme de deux nombres du même signe, alors ils sont normalement ajoutés et le résultat est placé un signe négatif:

(−20) + 9 + (−7) = (−11) + (−7) = −18

Signes dans le substitut

La soustraction de deux nombres est définie comme la somme de l'opposé. À son tour, le contraire d'un nombre est ledit numéro avec le signe modifié. Par exemple, l'opposé de 2 est (−2), l'opposé de (−5) est 5 et ainsi.

Dans cet esprit, lorsque vous avez la soustraction de deux nombres:

Un B

Il se transforme simplement en la somme de l'opposé de B:

A + (- b)

Et procéder comme décrit dans la section précédente. Remarque pour mettre un signe + un nombre négatif ne le modifie pas, mais très prudent, l'inverse n'est pas vrai.

Lorsque le nombre "A", qui est le Miniend, est supérieur au nombre "B", qui est volé, fonctionne comme dans la soustraction des nombres naturels. Pas de problème, car un grand nombre est soustrait d'une plus petite quantité:

Peut vous servir: inégalité du triangle: démonstration, exemples, exercices résolus

25 - 8 = 17

Avec les exemples suivants, la méthode d'ajouter le contraire à soustraire est très pratique:

(−5) - 24 = (−5) + (- 24) = - 29
32 - (−23) = 32 + 23 = 55

Loi des signes dans la multiplication

La loi des signes de multiplication est appliquée de cette manière:

• En multipliant deux nombres du même signe, le résultat est toujours positif.
• Le produit de deux nombres de signes opposés est toujours négatif.

Le résumé de la règle des signes pour la multiplication est montré dans l'image:

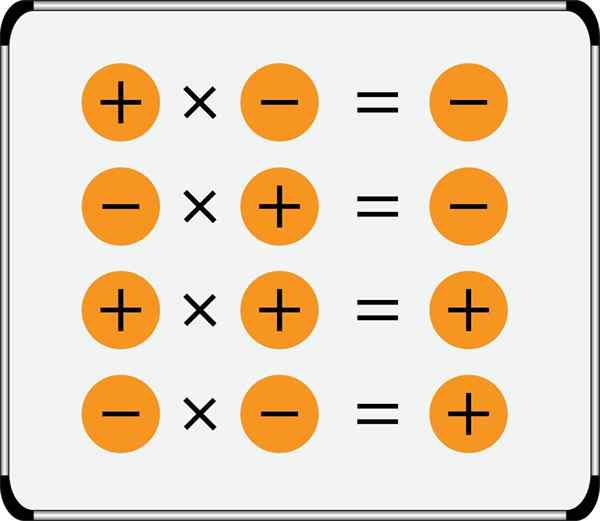
Notez que les nombres positifs peuvent être écrits sans le signe précédent, mais les nombres négatifs l'ont toujours, en outre, deux symboles arithmétiques ne sont jamais écrits les uns aux autres, ils doivent toujours être séparés par une parenthèse, par exemple:

Incorrect: 3 × −4
C'est Correct: 3 × (−4) = −12

(−5) × 6 = −5 × 6 = −30
(−3) × (−11) = 33
10 × 27 = 270

Pour multiplier plus de deux nombres, la propriété associative de la multiplication est utilisée, car l'ordre des facteurs ne modifie pas le produit, par exemple, lors de la réalisation:

(−2) × (−14) × 16

Vous pouvez multiplier les deux premiers facteurs, ou les deux derniers si vous le souhaitez, puis multiplier le résultat par le facteur restant. Dans ce cas, les deux facteurs seront multipliés en premier à partir de la gauche:

[(−2) × (−14)] × 16

Le produit de deux nombres négatifs est positif, alors (−2) × (−14) = 28 et reste:

28 × 16 = 448

Loi des signes dans la division

Il est analogue à la règle des signes de multiplication:

• Le rapport de deux nombres du même signe est toujours positif.
• En divisant deux numéros de signe autrement, le résultat est toujours négatif.

Il peut vous servir: différence entre cercle et circonférence (avec des exemples)

Par exemple:

24 ÷ 8 = 3
−36 ÷ 3 = −12
162 ÷ (−9) = −18
−216 ÷ (−6) = 36

Loi des signes dans l'autonomisation et le dépôt

Un exposant numéro écrit est:

pourⁿ

Où "a" est la base et "n" est l'exposant. Selon la parité de l'exposant: deux cas sont distingués:

Cas 1: A est positif

Lorsque la base est positive, le résultat est positif, que l'exposant soit uniforme ou impair, comme dans:

2³ = 8
3⁴ = 81

Cas 2: A est négatif

Voici deux cas:

• Lorsque l'exposant est égal, alors le résultat est positif.
• Si l'exposant est étrange, c'est négatif.

Exemples

3² = 3 ∙ 3 = 9
2³ = 2 ∙ 2 ∙ 2 = 8
(−2)⁴ = (−2) ∙ (−2) ∙ (−2) ∙ (−2) = 16
(−3)³ = (−3) ∙ (−3) ∙ (−3) = −27

Opérations avec des symboles de regroupement

Ils apparaissent souvent à des opérations distinctes avec des symboles de regroupement: parenthèses, supports et clés. Ceux-ci sont éliminés de l'intérieur en tenant compte de ce qui suit:

• Si un symbole de regroupement est précédé d'un signe positif, il peut être supprimé sans modifier les signes du contenu, par exemple: + (−3 + 5 - 1) = −3 + 5 - 1 = 1.
• Si un signe négatif précède le symbole de groupe, il est retiré en investissant le signe du contenu, par exemple: - (−3 + 5 −1) = 3 - 5 + 1 = −1.
• Lorsqu'il y a des opérations combinées de somme, de soustraction, de multiplication et de division, les propriétés associatives et distributives peuvent être utilisées pour la commodité.

Exercices résolus

a) 10 + 10

Solution: 20

b) (-8) + (-3)

Solution: -11

c) (3) + (-10) 

Solution: -7

d) (5) x (-3)

Solution: -15

e) (-10) x (-10)

Solution: 100

f) (18) ÷ (-3)

Solution: -6

G) (-10) ÷ (-2)

Solution: 5

h) 4 - (- 7 + 9)

Solution: 4 - (- 7 + 9) = 4 + 7 - 9 = 11− 9 = 2