Ellipse

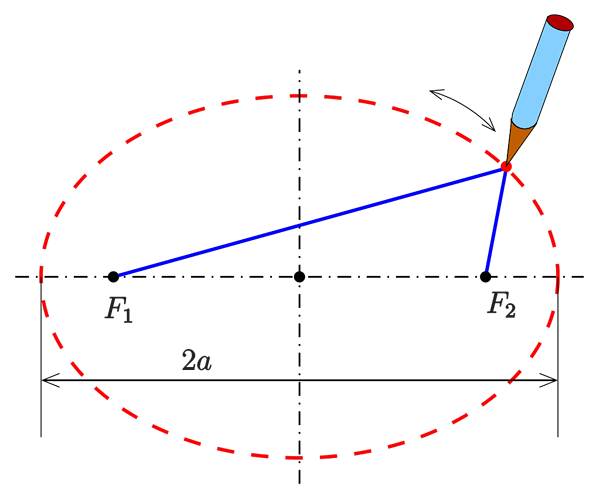
Figure 1. Méthode du jardinier pour dessiner une ellipse. La somme des distances entre un point p de l'ellipse (en rouge) et les projecteurs (en noir), reste constant. Source: Ag2Gaeh, CC BY-SA 4.0, via Wikimedia Commons.

Qu'est-ce qu'une ellipse?

Une ellipse est un ensemble de points de coordonnées (x, y), pour lequel la somme des distances à deux points fixes, appelés Focos, C'est constant. À son tour, les projecteurs sont séparés les uns des autres sur une distance égale à 2C.

Les ellipses se trouvent dans la nature. Par exemple, c'est dans le mouvement de la Terre autour du soleil, car comme démontré par l'astronomie allemande.

De plus, la forme elliptique se trouve dans la conception des constructions architecturales, fait partie d'un traitement médical pour détruire les calculs rénaux et sert à façonner divers objets tels que les réservoirs et autres conteneurs.

Dans la figure supérieure, une ellipse est représentée avec ses deux projecteurs, situé à équidistant du centre de la figure et sur l'axe le plus long. La condition qu'un point P doit se rencontrer pour appartenir à l'ellipse est que la somme des distances à chaque foyer est fixée:

d₁ + d₂ = constant.

Par conséquent, quand un jardinier veut. Ensuite, prenez une corde de bonne taille, attachez ses extrémités aux enjeux et soutenant un bâton sur la corde la glisse dessus pour marquer la rainure elliptique sur la terre douce. C'est lui méthode du jardinier Pour dessiner des ellipses.

Elipse Elements

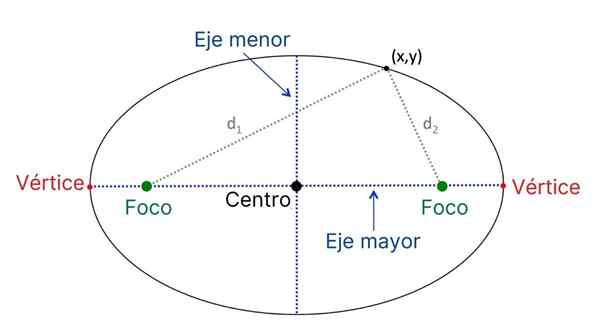Éléments principaux d'une ellipse

Ce sont les principaux éléments de l'ellipse:

1. Focos, Points fixes situés sur l'axe le plus long de l'ellipse.
2. Sommets, Ce sont les deux points de l'ellipse à travers lesquels la ligne passe qui rejoint les projecteurs.
3. Axe majeur, C'est la corde qui rejoint les sommets et contient également les projecteurs.
4. centre, Point central de l'axe majeur, qui correspond au point de coordonnées (H, K). Chaque orientation est équidistante du centre et à distance c du même.
5. Axe mineur, C'est la corde qui passe par le centre et est perpendiculaire à l'axe majeur.
6. Radios vectorielles, segments qui unissent chaque foyer avec un p de l'ellipse.
7. Axe focal, droit sur lequel les projecteurs sont.
8. Distance focale, C'est la distance entre les projecteurs, indiqué comme 2C.
9. Axe secondaire, axe perpendiculaire à l'axe majeur, qui est en même temps MediaTrix du segment qui se lie aux projecteurs.
10. Centre de symétrie, point coïncidant avec le centre de l'ellipse, où les axes de symétrie de la même chose sont croisés.
11. Axes de symétrie, lignes contenant les axes les plus grands et les plus petits de l'ellipse.

Peut vous servir: taxer

Types d'ellipse

Il existe deux types d'ellipse:

• Ceux qui ont l'axe principal horizontal.
• Ceux qui ont le plus grand axe vertical.

Ensuite, ils sont décrits mathématiquement:

Ellipse avec l'axe horizontal majeur

Laissez le point C des coordonnées (h, k) Le centre de l'ellipse, la longueur de l'axe majeur est 2a et la longueur de l'axe plus petit égal à 2b, avec un> b.

L'équation de cette ellipse est:

Ellipse avec l'axe vertical majeur

Avec les mêmes paramètres de l'ellipse avec un axe horizontal, l'ellipse avec l'axe vertical majeur est écrit comme:

Dans les deux cas, la distance entre la focalisation et le centre c Il est lié aux sédiments majeurs et mineurs à travers:

c² = A² - b²

Exemples d'ellipses

Ellipse horizontale

L'image suivante montre une ellipse dont le principal axe est horizontal. Le centre est au point (0,0) et les projecteurs en (-3,0) et (3,0) respectivement. Le point P (0, -4) mis en évidence appartient à l'ellipse.

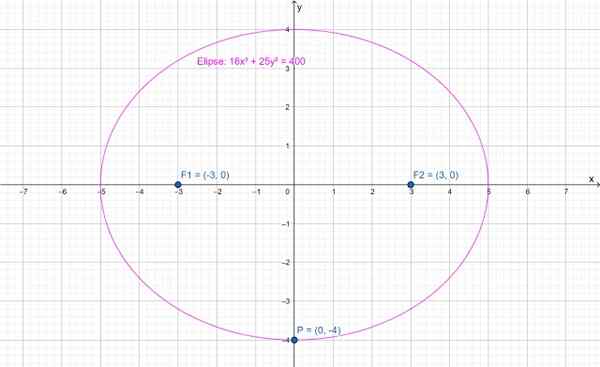Figure 2.- Ellipse dont le principal axe est horizontal. Source: F. Zapata à travers Geogebra.

L'équation de cette ellipse est:

16x² + 25 et² = 400

Il n'est pas difficile d'exprimer cette équation sous la forme canonique, il suffit de diviser tous les termes entre 400 et de simplifier facilement (voir l'exercice résolu plus tard).

Ellipse verticale

Ce qui suit est une ellipse verticale, dont l'axe majeur coïncide avec l'axe et. Il est axé sur le point (0,0) et son équation est:

36x² + 9Y² = 324

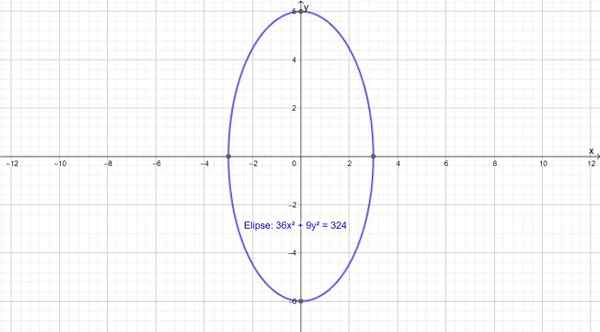figure 3.- Une ellipse avec l'axe vertical majeur. Source: F. Zapata à travers Geogebra.

Propriété de réflexion

Il se compose des éléments suivants: Si un réflecteur ou une source sonore est placé dans l'un des projecteurs d'ellipse, les ondes émises se reflètent vers l'autre focus. C'est un bon moyen de rediriger les vagues où votre énergie est nécessaire.

Peut vous servir: endecagon

C'est pourquoi dans les salles elliptiques, lorsqu'une personne parle à l'un des projecteurs, un auditeur situé dans l'autre foyer écoute clairement.

Et en médecine, cette propriété de réflexion est utilisée pour détruire les calculs rénaux en mettant le patient dans l'un des projecteurs d'une baignoire elliptique pleine d'eau, tandis que le générateur d'ondes à ultrasons est placé dans l'autre focus. Les vagues se reflètent dans les calculs et les fragment dans des particules plus petites, qui sont ensuite expulsées à travers l'urine.

La radio Ska

Ce radiotélescope est le plus grand de son type et devrait commencer à travailler en 2021. Sa surface est de 1 km carré et c'est pourquoi elle s'appelle Ska (en anglais, ils sont l'acronyme pour Tableau de kilomètre carré).

Profitant de la propriété de réflexion des ellipses, la structure consiste en un arrangement de 3000 antennes avec une forme elliptique d'environ 15 m de large, distribuée entre l'Australie et l'Afrique du Sud. Avec cet instrument, 50 fois plus sensible que ceux utilisés en ce moment, il devrait jeter un œil à l'univers alors qu'il était encore beaucoup plus jeune: environ un milliard d'années à peine.

Figure 4.- Interprétation artistique du Ska Radio Ska. Source: Wikimedia Commons.

Exercice résolu

Trouvez les équations canoniques des ellipses montrées sur les figures 2 et 3 et déterminez dans chaque cas les longueurs des sens plus importants et plus petits, ainsi que les distances focales.

Solution

Pour l'ellipse horizontal, dont l'équation est 16x² + 25 et² = 400, tous les termes entre 400 sont divisés, résultant:

Peut vous servir: dérivé de la cotangente: calcul, démonstration, exercices

 Qui est simplifié:

Le «A» semi-axe mesures 5 et les moindres mesures «B» 4, qui est également avertie en observant soigneusement l'image. Quant à la distance focale, vous devez:

c² = A² - b²

c² = 25 - 16 = 9 ⇒ c = √9 = 3

Par conséquent, C = 3 est la distance entre le centre et l'un des projecteurs. Les deux foyers sont une distance 2c = 6.

Quant à l'ellipse vertical 36x² + 9Y² = 324 Vous avez:

En simplifiant:

c² = 36 - 9 = 27

C = √27 ≅ 5.2

Par conséquent, la distance entre les projecteurs est de 10.4 unités.

Les références

1. Hoffman, J. Sélection de problèmes de mathématiques. Volume 3.
2. Stewart, J. 2006. Précaulement: mathématiques pour le calcul. 5e. Édition. Cengage Learning.
3. Formules d'univers. L'ellipse. Récupéré de: universoformules.com.
4. Wikipédia. Tableau de kilomètre carré. Récupéré de: est.Wikipédia.org.
5. Zill, D. 1984. Algèbre et trigonométrie. McGraw Hill.