Decagon régulier et irrégulier, propriétés, exemples

Il décagone C'est une figure plate avec un polygone en forme de 10 côtés et 10 sommets ou conseils. Les décagons peuvent être réguliers ou irréguliers, dans le premier cas, tous les côtés et les angles internes ont la même mesure, tandis que dans la seconde, les côtés et / ou les angles sont différents les uns des autres.

La figure 1 montre des exemples de décagons de chaque type et comme nous pouvons le voir, le décagon régulier est très symétrique.

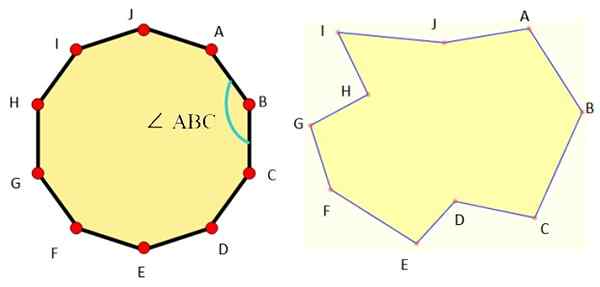Figure 1. À gauche un décagon régulier et à droite, un décagon irrégulier. Source: Wikimedia Commons / F. Zapata / MathpenRef.

Les éléments de base de tous les Decagon sont:

-Côtés, les segments de ligne qui se joignent au décagon.

-Sommets ou points entre chaque côté consécutif.

-Angles internes et externes entre les côtés adjacents.

-Diagonales, segments qui unissent deux sommets non consécutifs.

Les sommets sont appelés par des majuscules, comme le montre la figure 1, où les premières lettres de l'alphabet ont été utilisées, mais n'importe quelle lettre peut être utilisée.

Les côtés sont symbolisés par les deux lettres des sommets parmi lesquelles, par exemple, le côté ab est celui entre les sommets A et B. De la même manière que cela se fait avec les diagonales, nous avons donc la diagonale AF, qui rejoint les points A et F.

Pour les angles, nous utilisons ce symbole: ∠, similaire à un L incliné. Par exemple, l'angle ∠ ABC est celui dont le sommet est B et dont les côtés sont les segments AB et BC.

[TOC]

Decagon ordinaire

Dans le Decagon ordinaire, toutes les parties ont la même mesure, ainsi que les angles internes. Par conséquent, il est dit équilatéral (côtés égaux) et équiangle (Angles égaux). C'est une figure très symétrique

Angles intérieurs d'un décagon régulier

Pour trouver la mesure des angles internes d'un polygone ordinaire, y compris le décagon régulier, la formule suivante est utilisée:

Où:

-I est la mesure de l'angle en degrés.

-n est le nombre de côtés du polygone. Dans le cas de Decagon n = 10.

Peut vous servir: heptagone

Remplacement n = 10 Dans la formule précédente, nous obtenons ce qui suit:

Maintenant, on dit qu'un polygone est convexe Si ses mesures angulaires sont inférieures à 180 °, sinon le polygone est concave. Comme tout angle interne du décagon régulier mesure 144 ° et est inférieur à 180 °, alors c'est un polygone convexe.

Somme des angles internes

La somme des mesures des angles internes de tout polygone est, en degrés:

S = (n-2) x 180º; n est toujours supérieur à 2

Dans cette formule, nous devons:

-S est la somme des mesures des angles internes.

-n est le nombre de côtés. Pour le décagon n = 10

Application de la formule pour n = 10 résultats:

S = (10 - 2) x 180º = 1440º

Angles extérieurs 

Un angle extérieur se forme entre un côté et l'extension du côté adjacent, voyons:

Figure 2.- L'angle externe du décagon régulier mesure 36º. Fontaine. Wikimedia Commons / F. Zapata.

L'angle ∠ ABC plus l'angle externe ajoute 180 °, c'est-à-dire qu'ils sont Supplémentaire. Par conséquent, l'angle externe est égal à 180º-144º = 36º, comme nous le voyons sur la figure.

Nombre de diagonales

Comme indiqué précédemment, les diagonales sont les segments qui unissent les sommets non consécutifs. Combien de diagonales pouvons-nous tracer dans un décagon? Lorsque le nombre de sommets est petit, ils peuvent être facilement comptés, mais lorsque ce nombre augmente, vous pouvez perdre le compte.

Heureusement, il existe une formule pour connaître le nombre de diagonales d'un polygone n côtés:

Pour le décagon, nous remplaçons n = 10 et obtenons:

D = 10 x (10 - 3) / 2 = 35

Dans le Decagon ordinaire, toutes les diagonales sont coupées à un moment donné, qui est le centre de la figure:

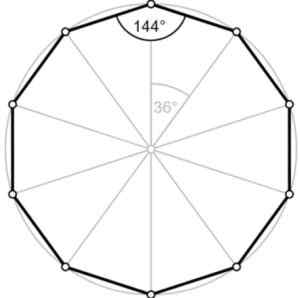figure 3. Angles et diagonales du décagon régulier. Source: Wikimedia Commons.

centre

Le centre d'un polygone est défini comme ce point équidistant de tout sommet. Dans la figure précédente, le centre coïncide avec le point d'intersection de toutes les diagonales.

Périmètre

Si le Decagon ordinaire a le côté A, son périmètre P est la somme de tous les côtés:

Peut vous servir: 90 diviseurs: quelles sont et explications

P = 10.pour

Zone

Connaître la longueur pour Sur le côté, la zone Decagon ordinaire est calculée par:

Une formule approximative pour la région est:

Et une troisième option pour trouver la zone est de la longueur de l'apothème L_POUR. C'est le segment qui rejoint le point médian d'un côté avec le centre du polygone.

Dans ce cas, la zone peut être calculée à l'aide de la formule:

Décrue irrégulière

Le décagon irrégulier n'est pas équilatéral ou équiangle, et en général il n'a pas la symétrie de la figure régulière, bien que certains décagons peuvent avoir un axe de symétrie.

Ils peuvent également être convex ou concaves, s'il y a des angles internes supérieurs à 180º.

Le décagone irrégulier de la figure 1 est concave, car certains de ses angles internes sont supérieurs à 180º. Il est évident qu'il existe de nombreuses combinaisons d'angles et de côtés qui donnent naissance à un décagon irrégulier.

En tout cas, il est réalisé que:

-Les angles internes d'un décagon irrégulier ajoutent également 1440º.

-Il a également 35 diagonales.

Zone d'un décagon irrégulier par Gauss Derminants

En général, il n'y a pas de formule unique pour trouver la zone d'un polygone irrégulier, car les côtés et les angles sont différents. Cependant, vous pouvez trouver la connaissance des coordonnées des sommets et le calcul du DÉTERMINANTS DE GAUSS:

-Appelons (x_n , et_n ) aux coordonnées des sommets, avec n variant de 1 à 10.

-Vous pouvez commencer à partir de n'importe quel sommet, à laquelle les coordonnées seront attribuées (x x₁, et₁ ). Vous devez maintenant remplacer les valeurs de chaque coordonnée dans cette formule:

Où les déterminants sont précisément les opérations entre parenthèses.

-Il est important de noter que le dernier déterminant implique le premier sommet avec le dernier. Pour le Decagon, ce serait comme ça:

(X_dixet₁ - X₁et_dix)

Peut vous servir: Interpolation de Lagrange

Important: Les barres sont celles d'une valeur absolue et signifient que le résultat final est toujours avec un signe positif.

La procédure peut être laborieuse lorsque le chiffre a de nombreux sommets, dans le cas du Decagon, il y a 10 opérations, il est donc conseillé de faire une table ou une liste.

Exercice résolu

Calculez la zone de décagon irrégulière illustrée sur la figure. Les coordonnées des sommets sont a, b, c ... j, dont les valeurs sont montrées à gauche.

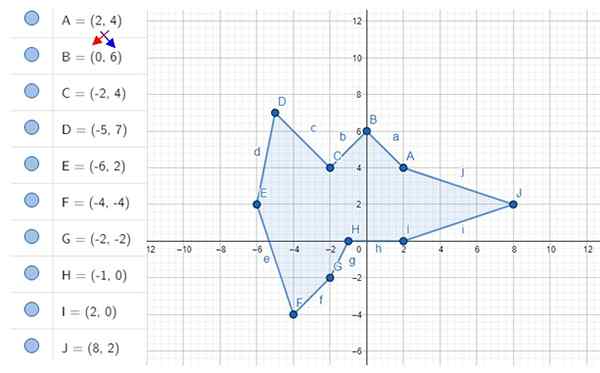Figure 4. Decagon irrégulier et ses sommets. Source: F. Zapata avec Geogebra.

Solution

-Nous faisons chacune des 10 opérations:

• 2 × 6 - 4 × 0 = 12 - 0 = 12
• 0 × 4 - 6 × (-2) = 0 + 12 = 12
• (-2) × 7- 4 × (-5) = -14 + 20 = 6
• (-5) × 2 -7 × (-6) = -10 + 42 = 32
• (-6) × (-4) -2 × (-4) = 24 + 8 = 32
• (-4) × (-2) - (- 4) × (-2) = 8-8 = 0
• (-2) × 0 - (- 2) × (-1) = 0 -2
• (-1) × 0 - 0 × (2) = 0 - 0 = 0
• 2 × 2 - 0 × 8 = 4 - 0 = 4
• 8 × 4 -2 × 2 = 32 - 4 = 28

-Nous ajoutons les résultats:

12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124

Un résultat positif est obtenu même sans les barres de valeur absolue, mais si elle est négative, la même chose est modifiée.

-Le résultat précédent est divisé par 2 et c'est la zone du polygone:

A = 124/2 = 62

Propriétés de Decangon

Vous trouverez ci-dessous le résumé des propriétés générales d'un décagon, qu'elle soit régulière ou irrégulière:

-A 10 côtés et 10 sommets.

-La somme des angles internes est de 1440º.

-Il y a 35 diagonales.

-Le périmètre est la somme de toutes les côtés.

-Vous pouvez créer des triangles à l'intérieur d'un polygone Dessin segments d'un sommet à tout le monde. Dans un décagon, il est possible de dessiner 8 triangles de cette manière, comme indiqué ci-dessous:

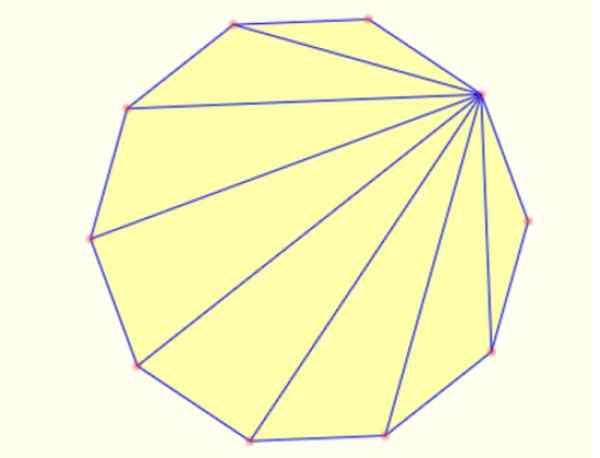Figure 5. Triangles internes dans un décagon régulier. Source: MathpenRef.

Les références

1. Alexander, D. 2013. Géométrie. 5e. Édition. Cengage Learning.
2. Décagone.com. Décagone. Récupéré de: Decagon.com
3. Référence ouverte en mathématiques. Décagone. Récupéré de: MathpenRef.com.
4. Mathématiques de Sangaku. Éléments d'un polygone et de sa classification. Récupéré de: Sangakoo.com.
5. Wikipédia. Décagone. Récupéré de: est.Wikipédia.com.