Concept de conception du coefficient, formule, calcul, exemple

Il coefficient de restitution C'est le quotient entre la vitesse de vitesse relative et la vitesse relative de l'approche de deux corps qui entrent en collision. Lorsque les corps sont unis après la collision, ce quotient est vide. Et l'unité vaut le cas où la collision est parfaitement élastique.

Supposons deux sphères de masse solides M1 et la masse M2 respectivement qu'ils subissent une collision. Juste avant la collision, les sphères avaient des vitesses V1 et V2 Concernant un certain système de référence inertielle. Juste après la collision, leurs vitesses changent V1 ' et V2 '.

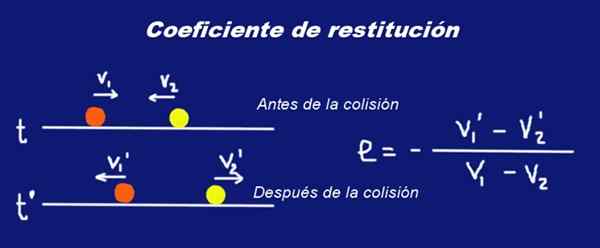Figure 1. Collision de deux sphères de masses M1 et M2 et leur coefficient de restitution et. Préparé par Ricardo Pérez.

La lettre a été placée caractère gras En vitesses pour indiquer que ce sont des quantités vectorielles.

Les expériences indiquent que chaque collision répond à la relation suivante:

V1 ' - V2 '= -et (V1 - V2)

Où et C'est un nombre réel entre 0 et 1, appelé le coefficient de restitution de la collision. L'expression précédente est interprétée comme suit: 

La vitesse relative de deux particules avant la collision est proportionnelle à la vitesse relative des deux particules après la collision, la constante de proportionnalité est (-e), où E est le coefficient de restitution de la collision.

[TOC]

Quel est le coefficient de restitution pour?

L'utilité de ce coefficient réside dans la connaissance du degré d'insélasticité d'une collision. Dans le cas où la collision est parfaitement élastique, le coefficient sera de 1, tandis que dans une collision complètement inélastique, le coefficient vaut 0, car dans ce cas, la vitesse relative après la collision est nul.

Réciproquement, si le coefficient de restitution d'une collision et que les vitesses des particules sont connues avant elle, alors les vitesses peuvent être prédites après une telle collision. 

Peut vous servir: 13 exemples de la première loi de Newton dans la vraie vie

L'élan

Dans les collisions, en plus de la relation établie par le coefficient de restitution, il existe une autre relation fondamentale, qui est la Conservation de l'élan.

L'élan p d'une particule ou d'une quantité de mouvement comme on l'appelle également, c'est le produit de la masse M de la particule pour sa vitesse V. C'est-à-dire: l'élan p C'est un montant vectoriel.

Dans les collisions, l'élan linéaire P Le système est le même juste avant et juste après la collision, car la force extérieure est méprisable contre les forces brèves mais intenses d'interaction interne pendant la collision. Mais la conservation de l'élan ne suffit pas P du système pour résoudre le problème général de la collision.

Dans le cas mentionné précédemment, celui des deux sphères M1 et M2 qui entrent en collision, la conservation de l'élan linéaire est écrite comme celle-ci:

 M1 V1 + M2 V2 = M1 V1 ' + M2 V2 ' .

Il n'y a aucun moyen de résoudre le problème de collision si le coefficient de restitution n'est pas connu. La conservation de l'élan, bien que nécessaire, est insuffisante pour prédire les vitesses après collision.

Lorsqu'un problème déclare que les corps se déplacent ensemble après la collision, dit implicitement que le coefficient de restitution est 0.

Figure 2. Dans les balles de billard, il y a des collisions de coefficient de restitution un peu moins de 1. Source: Pixabay.

Coefficient d'énergie et de restitution 

L'autre montant physique important impliqué dans les collisions est l'énergie. Pendant les collisions, il existe des échanges d'énergie cinétique, d'énergie potentielle et d'autres types d'énergie, comme l'énergie calorique.

Avant et après la collision, l'énergie potentielle de l'interaction est pratiquement nulle, donc le bilan énergétique implique l'énergie cinétique des particules avant et après et une quantité Q appelé énergie dissipée.

Cela peut vous servir: modèle atomique Heisenberg

Pour les deux sphères de masse M1 et M2 qui entrent en collision le bilan énergétique avant et après la collision, il est écrit comme ceci:

½ m1 V1^ 2 + ½ m2 V2^ 2 = ½ m1 V1 '^ 2 + ½ m2 V2 '^ 2 + Q

Lorsque les forces d'interaction pendant la collision sont purement conservatrices, il arrive que Énergie cinétique totale Parmi les particules qui entrent en collision. Lorsque cela se produit, on dit que la collision est parfaitement élastique.

En cas de collisions élastiques, l'énergie n'est pas dissipée. Et aussi le coefficient de restitution est conforme: E = 1. 

Au contraire, dans des collisions inélastiques qui ≠ 0 et 0 ≤ e < 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.

Pour qu'un problème de collision soit parfaitement déterminé, il est nécessaire de connaître le coefficient de restitution, ou alternativement la quantité d'énergie dissipée pendant la collision.

Le coefficient de restitution dépend de la nature et du type d'interaction entre les deux corps pendant la collision.

D'un autre côté, la vitesse relative des corps avant la collision définira l'intensité de l'interaction et donc son influence sur le coefficient de restitution. 

Comment le coefficient de restitution est-il calculé?

Pour illustrer comment le coefficient de restitution d'une collision est calculé, nous prendrons un cas simple:

Supposons la collision de deux sphères de masse M1 = 1 kg et M2 = 2 kg qui se déplacent sur un frottement droit (comme dans la figure 1).

La première sphère affecte la vitesse initiale V1 = 1 m / s À propos de la seconde qui est à l'origine au repos, c'est-à-dire V2 = 0 m / s.

Il peut vous servir: Première loi de la thermodynamique: formules, équations, exemples

Après la collision, ils se déplacent comme ceci: le premier s'arrête (V1 '= 0 m / s) Et le second se déplace vers la droite avec la vitesse V2 '= 1/2 m / s.

Pour calculer le coefficient de restitution dans cette collision, nous appliquons la relation:

V1 ' - V2 ' = -et ( V1 - V2 ) 

0 m / s - 1/2 m / s = - e (1 m / s - 0 m / s) => - 1/2 = - e => e = 1/2 .

Exemple

Dans la collision unique des deux sphères de la section précédente, son coefficient de restitution a été calculé, ce qui a entraîné E = ½ .

Comme e ≠ 1, la collision n'est pas élastique, c'est-à-dire l'énergie cinétique du système n'est pas conservée et il y a une certaine quantité d'énergie dissipée Q (par exemple le chauffage des sphères en raison de la collision).

Déterminez la valeur de l'énergie dissipée en joules. Calculez également la fraction en pourcentage de l'énergie dissipée.

Solution

L'énergie cinétique initiale de la sphère 1 est: 

K1i = ½ m1 v1 ^ 2 = ½ 1 kg (1 m / s) ^ 2 = ½ j

Tandis que celui de la sphère 2 est nul pour être initialement au repos.

Donc l'énergie cinétique initiale du système est ki = ½ j.

Après la collision, seule la deuxième sphère se déplace avec la vitesse V2 '= ½ m / s, donc l'énergie cinétique finale du système sera:

Kf = ½ m2 V2 '^ 2 = ½ 2 kg (½ m / s) ^ 2 = ¼ J

C'est-à-dire que l'énergie dissipée dans la collision est:

Q = ki - kf = (½ j - ¼ j) = 1/4 j

Et la fraction d'énergie dissipée dans cette collision est calculée comme suit:

F = q / ki = ¼ / ½ = 0,5 c'est-à-dire que 50% de l'énergie du système a été dissipée en raison de la collision inélastique dont le coefficient de restitution est de 0,5.

Les références

1. Bauer, w. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
2. Figueroa, D. 2005. Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique. Édité par Douglas Figueroa (USB).
3. Chevalier, r. 2017. Physique pour les scientifiques et l'ingénierie: une approche stratégique. Pearson.
4. Sears, Zemansky. 2016. Physique universitaire avec physique moderne. 14e. Élégant. Volume 1.
5. Wikipédia. Quantité de mouvement.Récupéré de: est.Wikipédia.org.